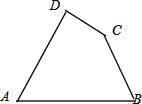
【题目】如图,四边形ABCD是一个工件的平面图,它要求AD和BC这两边的夹角应等于30°.甲、乙、丙三个工人在检验工件是否合格时,发生了以下争论:
甲:要检验工件是否合格,应延长AD和BC,设交点为O,然后检验∠O是否等于30°.
乙:这样太麻烦了,我看只需测量出∠A和∠B的度数就行了.
丙:量出∠C和∠D的度数也可以检验AD和BC的夹角是否等于30°.
请你用所学过的知识,说明乙、丙两人的方法是否正确.
参考答案:
【答案】乙、丙两人的方法都是正确的,理由详见解析.
【解析】
根据甲乙丙是三个工人的描述,通过三角形内角和为180°的定理进行分别证明即可.
解:乙、丙两人的方法都是正确的.如图,延长AD和BC,设交点为O,
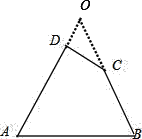
∵∠O=180°-∠A-∠B,
∴只需测量出∠A和∠B的度数,且∠A+∠B=150°就可以检验AD和BC的夹角等于30°;
∵∠O=180°-∠ODC-∠OCD=180°-(180°-∠ADC)-(180°-∠BCD)=∠ADC+∠BCD-180°,
∴只要量出∠C和∠D的度数,且∠C+∠D=210°,也可以检验AD和BC的夹角等于30°.
因此乙、丙两人的方法都是正确的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
-
科目: 来源: 题型:
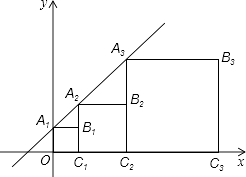
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示放置,点A1 , A2 , A3 , 和点C1 , C2 , C3 , …,分别在直线y=kx+b(k>0)和x轴上,已知点B1 , B2 , B3 , B4的坐标分别为(1,1)(3,2),(7,4),(15,8),则Bn的坐标是( )
A.(2n﹣1,2n﹣1)
B.(2n , 2n﹣1)
C.(2n﹣1 , 2n)
D.(2n﹣1﹣1,2n﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB>AC,AD平分∠BAC
(1)尺规作图:在AD上标出一点P,使得点P到点B和点C的距离相等(不写作法,但必须保留作图痕迹);
(2)过点P作PE⊥AB于点E,PF⊥AC于点F,求证:BE=CF;
(3)若AB=a,AC=b,则BE= ,AE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在三角形ABC中,点D在BC上,DE⊥AB于E,点F在AB上,在CF的延长线上取一点G,连接AG.
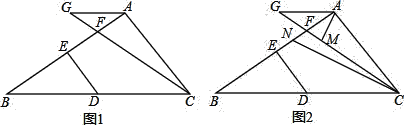
(1)如图1,若∠GAB=∠B,∠GAC+∠EDB=180°,求证:AB⊥AC.
(2)如图2.在(1)的条件下,∠GAC的平分线交CG于点M,∠ACB的平分线交AB于点N,当∠AMC-∠ANC=35°时,求∠AGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△
 的外角
的外角 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;
(2)若
 ,求
,求 的大小(用含
的大小(用含 的式子表示);
的式子表示);(3)用等式表示线段
 ,
,  与
与 之间的数量关系,并证明.
之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
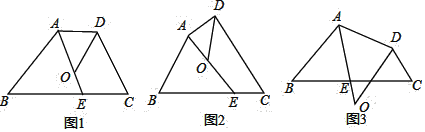
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
相关试题

