【题目】计算:
(1)﹣12+(﹣![]() )2﹣(π﹣3.14)0 (2)2x5·(﹣x)3+(﹣2x4)2
)2﹣(π﹣3.14)0 (2)2x5·(﹣x)3+(﹣2x4)2
(3)(x+5)(x﹣3)﹣x(x﹣2) (4)(2x﹣1)(2x+1)﹣(x﹣1)2
参考答案:
【答案】(1)7;(2)2x8 ;(3)4x-15 ;(4)3x2+2x-2
【解析】试题分析:(1)根据有理数的乘法法则,零指数幂的意义计算即可;
(2)用单项式乘以单项式和积的乘方法则计算即可;
(3)利用多项式乘以多项式和单项式乘以多项式法则计算后,合并同类项即可;
(4)利用乘法公式计算后,合并同类项即可.
试题解析:解:(1)原式=﹣1+9-1 =7;
(2)原式=2x5·(﹣x3)+4x8 =![]() =2x8 ;
=2x8 ;
(3)原式=x2+2x-15-x2+2x =4x-15;
(4)原式=4x2-1-(x2-2x+1)=4x2-1-x2+2x-1=3x2+2x-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于( )
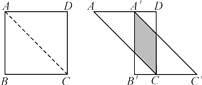
A. 4 cm B. 8 cm C. 6 cm D. 4 cm或8 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作示例:如图1,在△ABC中,AD为BC边上的中线,△ABD的面积记为S1,△ADC的面积记为S2.则S1=S2.


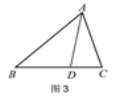

解决问题:在图2中,点D、E分别是边AB、BC的中点,若△BDE的面积为2,则四边形ADEC的面积为 .
拓展延伸:
(1)如图3,在△ABC中,点D在边BC上,且BD=2CD,△ABD的面积记为S1,△ADC的面积记为S2.则S1与S2之间的数量关系为 .
(2)如图4,在△ABC中,点D、E分别在边AB、AC上,连接BE、CD交于点O,且BO=2EO,CO=DO,若△BOC的面积为3,则四边形ADOE的面积为 .
-
科目: 来源: 题型:
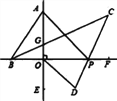
查看答案和解析>>【题目】如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,
AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.
(1)求∠BGO的度数;
(2)试确定∠C与∠OAP之间的数量关系,并说明理由;
(3)P在直线上运动,∠C+∠D的值是否变化?若发生变化,说明理由;若不变求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)

-
科目: 来源: 题型:
查看答案和解析>>【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出___只粽子,利润为___元;
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经学习了一元二次方程的四种解法:因式分解法、直接开平方法、配方法和公式法.请选择合适的方法解下列方程.
(1)x2-3x+1=0;
(2)(x-1)2=3;
(3)x2-3x=0;
(4)x2-2x=4.
相关试题

