【题目】如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于( )
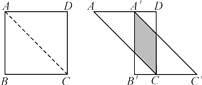
A. 4 cm B. 8 cm C. 6 cm D. 4 cm或8 cm
参考答案:
【答案】D
【解析】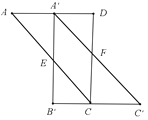
设AA′=xcm,则A′D=(12-x)cm,∵正方形ABCD,∴∠D=90°,AD=CD,∴∠DAC=45°,同理可证∠B′A′C′=45°,∵△A′B′C′由△ABC沿着AD方向平移得到,∴A′B′⊥AD,∴∠A′EA=45°,∴∠B′A′C′=∠A′EA,∴A′F∥EC,∵A′E∥CF,∴四边形A′ECF为平行四边形,所以SA′ECF= A′E×A′D=x(12-x)=32,解得x=4或8.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解广大市民对垃圾分类知识的了解程度,应采用的合适的调查方式为_________.(填普查或抽样调查)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠ABE与∠CDE的角平分线相交于点F,若∠F=125°,则∠E的度数为( )

A. 110° B. 120° C. 115° D. 105°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】操作示例:如图1,在△ABC中,AD为BC边上的中线,△ABD的面积记为S1,△ADC的面积记为S2.则S1=S2.


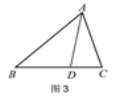

解决问题:在图2中,点D、E分别是边AB、BC的中点,若△BDE的面积为2,则四边形ADEC的面积为 .
拓展延伸:
(1)如图3,在△ABC中,点D在边BC上,且BD=2CD,△ABD的面积记为S1,△ADC的面积记为S2.则S1与S2之间的数量关系为 .
(2)如图4,在△ABC中,点D、E分别在边AB、AC上,连接BE、CD交于点O,且BO=2EO,CO=DO,若△BOC的面积为3,则四边形ADOE的面积为 .
-
科目: 来源: 题型:
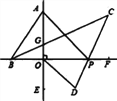
查看答案和解析>>【题目】如图,直线AE⊥BF于O,将一个三角板ABO如图放置(∠BAO=30°),两直角边与直线BF,
AE重合,P为直线BF上一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE.
(1)求∠BGO的度数;
(2)试确定∠C与∠OAP之间的数量关系,并说明理由;
(3)P在直线上运动,∠C+∠D的值是否变化?若发生变化,说明理由;若不变求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣12+(﹣
 )2﹣(π﹣3.14)0 (2)2x5·(﹣x)3+(﹣2x4)2
)2﹣(π﹣3.14)0 (2)2x5·(﹣x)3+(﹣2x4)2(3)(x+5)(x﹣3)﹣x(x﹣2) (4)(2x﹣1)(2x+1)﹣(x﹣1)2
相关试题

