【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,
(1)如图1, 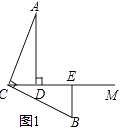
①线段CD和BE的数量关系是;
②请写出线段AD,BE,DE之间的数量关系 .
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系. 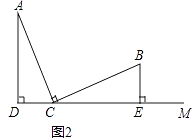
参考答案:
【答案】
(1)CD=BE;AD=BE+DE
(2)解:②中的结论不成立.结论:DE=AD+BE.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,
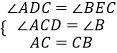 ,
,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∵DE=CD+CE=BE+AD,
∴DE=AD+BE.
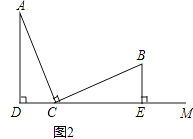
【解析】解:(1)①结论:CD=BE. 理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,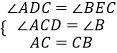 ,
,
∴△ACD≌△CBE,
∴CD=BE.
②结论:AD=BE+DE.
理由:∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵CE=CD+DE=BE+DE,
∴AD=BE+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°③
 (∠α+∠β);④
(∠α+∠β);④ (∠α﹣∠β).正确的有( )
(∠α﹣∠β).正确的有( )A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=130°,∠COD=80°,OM,ON分别是∠AOB和∠COD的平分线.
(1)如果OA,OC重合,且OD在∠AOB的内部,如图1,求∠MON的度数;
(2)如果将图1中的∠COD绕点O点顺时针旋转n°(0<n<155),如图2,
①∠MON与旋转度数n°有怎样的数量关系?说明理由;
②当n为多少时,∠MON为直角?
(3)如果∠AOB的位置和大小不变,∠COD的边OD的位置不变,改变∠COD的大小;将图1中的OC绕着O点顺时针旋转m°(0<m<100),如图3,∠MON与旋转度数m°有怎样的数量关系?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.
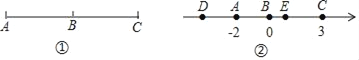
回答问题:
(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.
①若A是线段DB的中点,则点D表示的数是 ;
②若E是线段AC的中点,求点E表示的数.
(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.
①若点P表示的数是1,则m、n可能的值是 (填写符合要求的序号);
(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2
②直接用含m、n的代数式表示点P表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3“分裂”后,其中有一个奇数是347,则m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了
 如图,作一个
如图,作一个 ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分 .
.你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:
 中,______
中,______ ______,______
______,______ ______,______
______,______ ______.
______.求证:OP平分
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,放在平面直角坐标系中的圆O的半径为3,现做如下实验:抛掷一枚均匀的正四面体骰子,它有四个顶点,各顶点数分别是1,2,3,4,每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
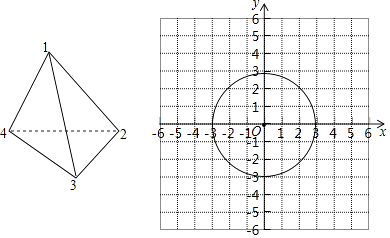
(1)若第一次骰子朝上的点数为1,第二次骰子朝上的点数为2,此时点P(填“是”或“否”)落在圆O内部;
(2)请你用树状图或列表的方法表示出P点坐标的所有可能结果;
(3)求点P落在圆O面上(含内部与边界)的概率.
相关试题

