搜索
【题目】线段MN在直角坐标系中的位置如图所示，若线段M′N′与MN关于y轴对称，则点M的对应点M′的坐标为（ ）
A.（4，2）
B.（﹣4，2）
C.（﹣4，﹣2）
D.（4，﹣2）
参考答案：
【答案】D
【解析】解：根据坐标系可得M点坐标是（﹣4，﹣2），
故点M的对应点M′的坐标为（4，﹣2），
故选：D．
【考点精析】本题主要考查了坐标与图形变化-对称的相关知识点，需要掌握关于x轴对称的点的特征：两个点关于x轴对称时，它们的坐标中，x相等，y的符号相反，即点P（x，y）关于x轴的对称点为P’（x，-y）；关于y轴对称的点的特征：两个点关于y轴对称时，它们的坐标中，y相等，x的符号相反，即点P（x，y）关于y轴的对称点为P’（-x，y）才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格中，△ABC各顶点都在格点上，点A，C的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC关于y轴对称的△A1B1C1；
（2）画出△ABC关于原点O对称的△A2B2C2；
（3）点C1的坐标是；点C2的坐标是；过C、C1、C2三点的圆的圆弧
的长是（保留π）． -
科目： 来源： 题型：
查看答案和解析>>【题目】解答题
（1）如图（1）点P是正方形ABCD的边CD上一点（点P与点C，D不重合），点E在BC的延长线上，且CE=CP，连接BP，DE．求证：△BCP≌△DCE；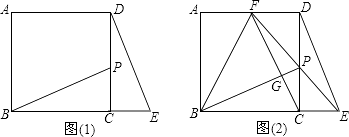
（2）直线EP交AD于F，连接BF，FC．点G是FC与BP的交点． ①若CD=2PC时，求证：BP⊥CF；
②若CD=nPC（n是大于1的实数）时，记△BPF的面积为S1 ， △DPE的面积为S2 ． 求证：S1=（n+1）S2 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数的图象与x轴相交于点A（﹣3，0）、B（﹣1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx﹣4k（k≠0）的图象过点P交x轴于点Q．
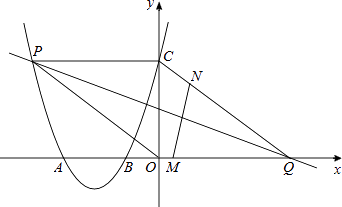
（1）求该二次函数的解析式；
（2）当点P的坐标为（﹣4，m）时，求证：∠OPC=∠AQC；
（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．
①连接AN，当△AMN的面积最大时，求t的值；
②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，且AC在直线l上，将△ABC绕点A顺时针旋转到①，可得到点P1 ， 此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2 ， 此时AP2=2+
；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3 ， 此时AP3=3+ ；…按此规律继续旋转，直到点P2012为止，则AP2012等于（ ） 
A.2011+671
B.2012+671
C.2013+671
D.2014+671 -
科目： 来源： 题型：
查看答案和解析>>【题目】无论a取什么实数，点P（a﹣1，2a﹣3）都在直线l上．Q（m，n）是直线l上的点，则（2m﹣n+3）2的值等于 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）|﹣1|+（﹣2）2+（7﹣π）0﹣（
）﹣1
（2）
÷ 
﹣ 
× 
+ 
．
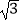相关试题
