【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1 , 此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=2+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=3+ ![]() ;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
;…按此规律继续旋转,直到点P2012为止,则AP2012等于( ) 
A.2011+671 ![]()
B.2012+671 ![]()
C.2013+671 ![]()
D.2014+671 ![]()
参考答案:
【答案】B
【解析】解:∵Rt△ABC中,∠ACB=90°,∠B=30°,AC=1, ∴AB=2,BC= ![]() ,
,
∴将△ABC绕点A顺时针旋转到①,可得到点P1 , 此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2 , 此时AP2=2+ ![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3 , 此时AP3=2+ ![]() +1=3+
+1=3+ ![]() ;
;
又∵2012÷3=670…2,
∴AP2012=670(3+ ![]() )+2+
)+2+ ![]() =2012+671
=2012+671 ![]() .
.
故选:B.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:△BCP≌△DCE;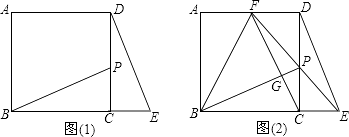
(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点. ①若CD=2PC时,求证:BP⊥CF;
②若CD=nPC(n是大于1的实数)时,记△BPF的面积为S1 , △DPE的面积为S2 . 求证:S1=(n+1)S2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx﹣4k(k≠0)的图象过点P交x轴于点Q.
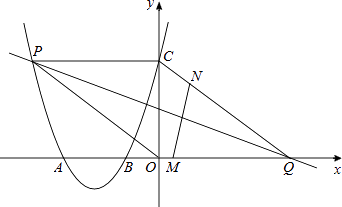
(1)求该二次函数的解析式;
(2)当点P的坐标为(﹣4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )

A.(4,2)
B.(﹣4,2)
C.(﹣4,﹣2)
D.(4,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】无论a取什么实数,点P(a﹣1,2a﹣3)都在直线l上.Q(m,n)是直线l上的点,则(2m﹣n+3)2的值等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|﹣1|+(﹣2)2+(7﹣π)0﹣( )﹣1
)﹣1
(2) ÷
÷ 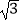 ﹣
﹣  ×
×  +
+  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加家务劳动的情况,某中学随机抽取部分学生,统计他们双休日两天家务劳动的时间,将统计的劳动时间(单位:分钟)分成5组:30≤x<60,60≤x<90,90≤x<120,120≤x<150,150≤x<180,绘制成频数分布直方图.请根据图中提供的信息,解答下列问题:
(1)这次抽样调查的样本容量是;
(2)根据小组60≤x<90的组中值75,估计该组中所有数据的和为;
(3)该中学共有1000名学生,估计双休日两天有多少名学生家务劳动的时间不小于90分钟?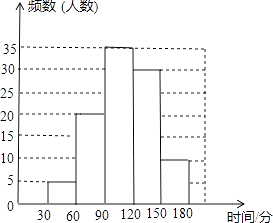
相关试题

