【题目】一次函数y=(k－)x－3k+10（k为偶数）的图象经过第一、二、三象限，与x轴、y轴分别交于A、B两点，过点B作一直线与坐标轴围成的三角形面积为2，交x轴于点C.

（1）求该一次函数的解析式；

（2）若一开口向上的抛物线经过点A、B、C三点，求此抛物线的解析式。

（3）过（2）中的A、B、C三点作△ABC，求tan∠ABC的值.

参考答案：

【答案】（1）（2）（3）

【解析】

试题分析：（1）求该一次函数y=（k-）x-3k+10（k为偶数）的解析式，需求出k的值，根据图象经过第一、二、三象限，得到k的取值范围，确定k的值，得到一次函数的解析式为y=x+4．

（2）求抛物线的解析式，可用待定系数法，需要求出A，B，C三点的坐标，

先根据一次函数的解析式求出A、B两点的坐标，再由S△BOC=2，求出C点坐标．

（3）要求tan∠ABC的值，根据正切函数的定义，构造一个以∠ABC为内角的直角三角形，过C作CD⊥AB于D，则tan∠ABC=．由于已知A、B、C三点的坐标，可根据三角函数的定义分别求出DC，AD的值，再算出BD的值．

试题解析：⑴（4分）由题意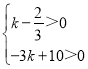得：，解得，又k为偶数

∴k＝2∴一次函数的解析式为

⑵（4分）求得A(－3，0)、B(0，4)，∴OB＝4

∵＝2OC＝2，∴OC＝1

∴C(1，0)或(－1，0)

若取C(1，0)、A(－3，0)、B(0，4)，设y＝a(x＋3)(x-1)，

将B(0，4)代入，求得，舍.

若取C(-1，0)、A(－3，0)、B(0，4)，设y＝a(x＋3)(x+1)，

将B(0，4)代入，求得，

∴抛物线为

⑶（4分）如图，过C作CD⊥AB于D，则tan∠ABC＝

∵ Sin∠BAO＝，cos∠BAO＝

∴ ， DC＝，，AD＝，∴BD＝

∴ tan∠ABC＝ （用相似证明也对）

关闭