【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
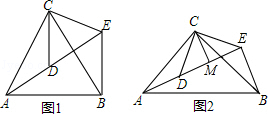
参考答案:
【答案】(1)60°;(2)∠AEB=90°AE= BE+2CM.
【解析】解:(1)∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°﹣∠DCB =∠BCE.
在△ACD和△BCE中,
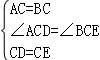 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
(2)
∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°
∴CA=CB,CD=CE.
且∠ACD=∠BCE.
在△ACD和△BCE中,
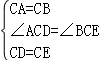 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 80° B. 90° C. 100° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (2016湖北随州第12题)已知等腰三角形的一边长为9,另一边长为方程x2﹣8x+15=0的根,则该等腰三角形的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的立方根是1,则这个数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. m2+m=3m3 B. (m2)3 =m5 C. (2m)2 =2m2 D. m ·m2=m3
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+kx-3=0的一个根是x=1,则另一个根是;
-
科目: 来源: 题型:
查看答案和解析>>【题目】解一元二次方程x2﹣8x﹣5=0,用配方法可变形为( )
A.(x+4)2=11
B.(x﹣4)2=11
C.(x+4)2=21
D.(x﹣4)2=21
相关试题

