【题目】如图,圆心角∠AOB=120°,弦AB=2 ![]() cm.
cm.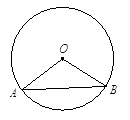
(1)求⊙O的半径r;
(2)求劣弧 ![]() 的长(结果保留
的长(结果保留 ![]() ).
).
参考答案:
【答案】
(1)解:作OC⊥AB于C,则AC= ![]() AB=
AB= ![]() cm.
cm.
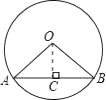
∵∠AOB=120°,OA=OB∴∠A=30°.
∴在Rt△AOC中,r=OA= ![]() =2cm
=2cm
(2)解:劣弧AB的长= ![]() πr=
πr= ![]() πcm
πcm
【解析】(1)根据垂径定理求出AC的值,由∠AOB的值,求出∠A的度数,根据三角函数求出⊙O的半径r;(2)根据弧长公式l=![]() πr,求出劣弧AB的长.
πr,求出劣弧AB的长.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)已知:sinα·cos60=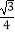 ,求锐角α;
,求锐角α;
(2)计算: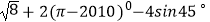 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲处表示两条路的交叉口,乙处也是两条路的交叉口,如果用(1,3)表示甲处的位置,那么“(1,3)→(2,3)→(3,3)→(4,3)→(4,2)→(4,1)→(4,0)”表示甲处到乙处的一种路线,若图中一个单位长度表示5Km,请你用上述表示法写出甲处到乙处的另两种走法,最短距离是多少千米?
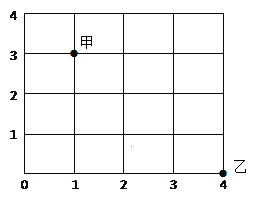
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系中,点
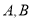 的坐标分别是
的坐标分别是 且
且 .
.
(1)求
 的值;
的值;(2)在
 轴上是否存在点
轴上是否存在点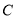 ,使三角形
,使三角形 的面积是
的面积是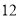 ?若存在,求出点
?若存在,求出点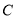 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)已知点
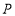 是
是 轴正半轴上一点,且到
轴正半轴上一点,且到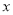 轴的距离为
轴的距离为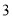 ,若
,若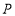 点沿
点沿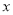 轴负半轴方向以每秒
轴负半轴方向以每秒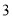 个单位长度平移至点
个单位长度平移至点 ,当运动时间
,当运动时间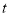 为多少秒时,四边形
为多少秒时,四边形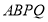 的面积
的面积 为
为 个平方单位?并写出此时点
个平方单位?并写出此时点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面
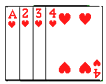
(1)从中随机抽出一张牌,试求出牌面数字是偶数的概率;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.

A. 1080 B. 900 C. 600 D. 108
-
科目: 来源: 题型:
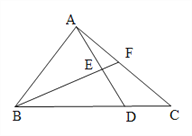
查看答案和解析>>【题目】如图,△ABC的面积为49cm2,AE=ED,BD=3DC,则图中△AEF的面积等于___________.
相关试题

