【题目】如图,在△ABC中,AB=AC=6,∠BAC=120°,点D是AB边上的点, ![]() =
= ![]() ,点P为底边BC上的一动点,则△PDA周长的最小值为 .
,点P为底边BC上的一动点,则△PDA周长的最小值为 . 
参考答案:
【答案】2 ![]() +2
+2
【解析】解:∵AB=AC=6, ![]() =
= ![]() , ∴AD=2,BD=4,
, ∴AD=2,BD=4,
作A关于BC的对称点A′,连接DA′交BC于P,
则DA′=PD+PA的最小值,
过A′作A′H⊥AB于H,
∵∠BAC=120°,
∴∠BAA′=60°,∠B=∠C=30°,
∴AA′=6,A′H=3 ![]() ,
,
∴DH=3﹣2=1,
∴A′D= ![]() =2
=2 ![]() ,
,
∴△PDA周长的最小值=2 ![]() +2,
+2,
所以答案是:2 ![]() +2.
+2.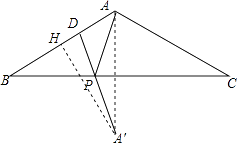
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
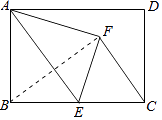
查看答案和解析>>【题目】在矩形ABCD中,AB=6,AD=10,点E是边BC的中点,连接AE,若将△ABE沿AE翻折,点B落在点F处,连接FC,则tan∠BCF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOB是一条直线,OC是∠AOD的平分线,OE 是∠BOD的平分线.

(1)若∠AOE=140°,求∠AOC的度数;
(2)若∠EOD :∠COD=2 : 3,求∠COD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|1﹣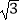 |+(﹣1)2017﹣(3﹣π)0
|+(﹣1)2017﹣(3﹣π)0
(2)(1﹣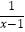 )÷
)÷ 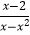 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
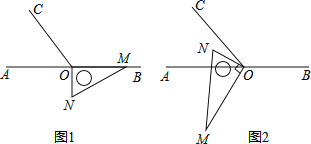
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)解方程组 ;
;
(2)解不等式: <4﹣
<4﹣ 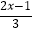 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
相关试题

