[题目]如图.已知AOB是一条直线.OC是∠AOD的平分线.OE 是∠BOD的平分线. (1)若∠AOE=140°.求∠AOC的度数,(2)若∠EOD :∠COD=2 : 3.求∠COD的度数. 题目和参考答案 ——青夏教育精英家教网—

【题目】如图，已知AOB是一条直线，OC是∠AOD的平分线，OE 是∠BOD的平分线.

（1）若∠AOE=140°，求∠AOC的度数；

（2）若∠EOD :∠COD=2 : 3，求∠COD的度数.

参考答案：

【答案】（1）50°（2）54°

【解析】试题分析：（1）根据角平分线的性质，由角的和差关系求解即可；

（2）根据比例关系，设出未知数，然后根据和为90°，列方程求解即可.

试题解析：（1）OC是∠AOD的平分线，OE是∠BOD的平分线，

∠DOE=∠BOD，∠COD=∠AOD， ∠AOB=180°，

∠COE=∠DOE+∠COD=∠BOD+∠AOD=∠AOB=90°，

∠AOC=∠AOE-∠EOC=140°-90°=50°．

（2）∠COE=90°，∠EOD :∠COD=2 : 3，

设∠EOD=2x°，∠COD=3x°，2x+3x=90， x=18， ∠COD=54°．

相关试题

科目： 来源： 题型：

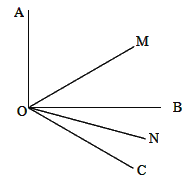
【题目】如图，∠AOB＝90°，∠BOC＝60°，射线OM平分∠AOC，ON平分∠BOC。
（1）求∠MON的度数；
（2）如果（1）中，∠AOB＝α，∠BOC＝β（β为锐角），其他条件不变，求∠MON的度数；
（3）从（1）、（2）的结果中，你能得到什么规律？
查看答案和解析>>
科目： 来源： 题型：

【题目】下面说法：①平面内，过一点有且只有一条直线与已知直线垂直；②对顶角相等；③两条直线被第三条直线所截，同位角相等；④从直线外一点到这条直线的垂线段叫做点到直线的距离，其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目： 来源： 题型：

【题目】在以下现象中，属于平移的是( )
①在荡秋千的小朋友； ②电梯上升过程；
③宇宙中行星的运动； ④生产过程中传送带上的电视机的移动过程．
A.②④B.①②C.②③D.③④
查看答案和解析>>
科目： 来源： 题型：

【题目】如图5，O为直线AB上一点， ∠AOC=48°,OE平分∠AOC, ∠DOE=90°
(1)求∠BOE的度数。
(2)试判断OD是否平分∠BOC？试说明理由。
查看答案和解析>>
科目： 来源： 题型：

【题目】背景资料:
在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小．
这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．
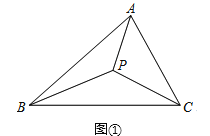
如图①，当△ABC三个内角均小于120°时，费马点P在△ABC内部，此时∠APB＝∠BPC＝∠CPA＝120°，此时，PA＋PB＋PC的值最小．
解决问题：
（1）如图②，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP′≌△ABP，这样就可以利用旋转变换，将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB=　　；
基本运用：
（2）请你利用第（1）题的解答思想方法，解答下面问题：
如图③，△ABC中，∠CAB=90°，AB=AC，E，F为BC上的点，且∠EAF=45°，判断BE，EF，FC之间的数量关系并证明；
能力提升：
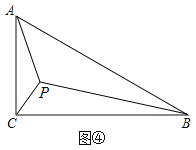
（3）如图④，在Rt△ABC中，∠C=90°，AC=1，∠ABC=30°，点P为Rt△ABC的费马点，
连接AP，BP，CP，求PA+PB+PC的值．

查看答案和解析>>
科目： 来源： 题型：

【题目】定义：对于给定的两个函数，任取自变量x的一个值，当x＜0时，它们对应的函数值互为相反数；当x≥0时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：一次函数y=x﹣1，它的相关函数为．
（1）已知点A（﹣5，8）在一次函数y=ax﹣3的相关函数的图象上，求a的值；
（2）已知二次函数．
①当点B（m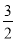，）在这个函数的相关函数的图象上时，求m的值；
②当﹣3≤x≤3时，求函数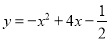的相关函数的最大值和最小值；
（3）在平面直角坐标系中，点M，N的坐标分别为（﹣，1），（，1}），连结MN．直接写出线段MN与二次函数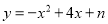的相关函数的图象有两个公共点时n的取值范围．
查看答案和解析>>