【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.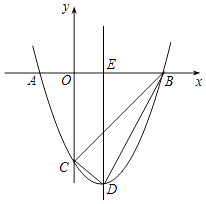
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
参考答案:
【答案】
(1)
解:把A(﹣1,0)和B(3,0)两点代入抛物线y=x2+bx+c中得:
![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为:y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴C(0,﹣3),D(1,﹣4),
由勾股定理得:BC2=32+32=18,
CD2=12+(4﹣3)2=2,
BD2=(3﹣1)2+42=20,
∴CD2+BC2=BD2,
即∠BCD=90°,
∴△BCD是直角三角形
(2)
解:作PQ⊥OC于点Q,
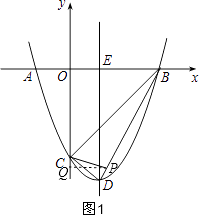
∴∠PQC=90°,
∵∠PCO+∠CDB=180°,
∠PCO+∠PCQ=180°,
∴∠CDB=∠PCQ,
∵∠PQC=∠BCD=90°,
∴△PCQ∽△BDC,
∴ ![]() =3,
=3,
∴PQ=3CQ,
设CQ=m,则PQ=3m,
设P(3m,﹣3﹣m),
设直线BD的解析式为:y=kx+b,
把B(3,0)、D(1,﹣4)代入得: ![]() ,
,
解得: ![]() ,
,
∴直线BD的解析式为:y=2x﹣6,
将点P的坐标代入直线BD:y=2x﹣6得:
﹣3﹣m=2×3m﹣6,
m= ![]() ,
,
∴3m= ![]() ,﹣3﹣m=﹣3﹣
,﹣3﹣m=﹣3﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() );
);
(3)
解:∵∠CMN=∠BDE,
∴tan∠BDE=tan∠CMN= ![]() =
= ![]() ,
,
∴ ![]() ,
,
同理可求得:CD的解析式为:y=﹣x﹣3,
设N(a,﹣a﹣3),M(x,x2﹣2x﹣3),
①如图2,过N作GF∥y轴,过M作MG⊥GF于G,过C作CF⊥GF于F,
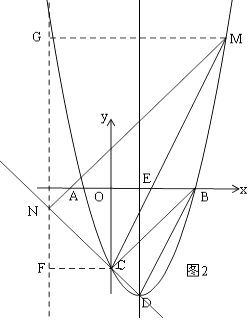
则△MGN∽△NFC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =2,
=2,
则 ![]() ,
,
∴x1=0(舍),x2=5,
当x=5时,x2﹣2x﹣3=12,
∴M(5,12),
②如图3,过N作FG∥x轴,交y轴于F,过M作MG⊥GF于G,
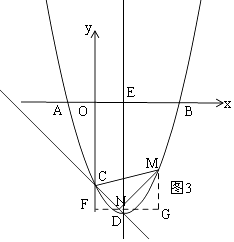
∴△CFN∽△NGM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
则 ![]() ,
,
∴x1=0(舍),x2= ![]() ,
,
当x= ![]() 时,y=x2﹣2x﹣3=﹣
时,y=x2﹣2x﹣3=﹣ ![]() ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
综上所述,点M的坐标(5,12)或( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)先利用待定系数法求二次函数的解析式,并配方成顶点式求顶点D的坐标,和与y轴的交点C的坐标,由勾股定理计算△BDC三边的平方,利用勾股定理的逆定理证明△BCD是直角三角形;(2)作辅助线,构建直角三角形PCQ与直角三角形BDC相似,根据比例式表示出点P的坐标,利用待定系数法求直线BD的解析式,因为点P为线段BD上一点,代入直线BD的解析式列方程可求出点P的坐标;(3)同理求直线CD的解析式为:y=﹣x﹣3,由此表示点N的坐标为(a,﹣a﹣3),因为M在抛物线上,所以设M(x,x2﹣2x﹣3),根据同角的三角函数得:tan∠BDE=tan∠CMN= ![]() ,则
,则 ![]() ,
,
如图2,证明△MGN∽△NFC,列比例式可得方程组解出即可;
如图3,证明△CFN∽△NGM,列比例式可得方程组解出即可.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
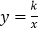 与一次函数
与一次函数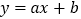 的图象交于点A(-2,6)、点B(
的图象交于点A(-2,6)、点B(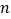 ,1).
,1).(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
(3)将一次函数
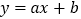 的图象沿
的图象沿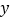 轴向下平移n个单位,使平移后的图象与反比例函数
轴向下平移n个单位,使平移后的图象与反比例函数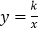 的图象有且只有一个交点,求n的值.
的图象有且只有一个交点,求n的值.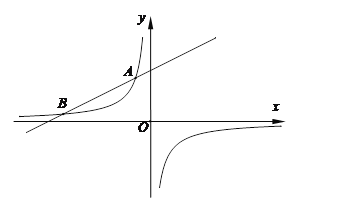
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
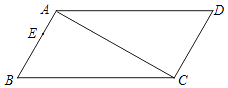
(1)求证四边形ABCD是平行四边形;
(2)当△BEP为等腰三角形时,求t2﹣31t的值;
(3)当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与ABCD重叠部分的面积. -
科目: 来源: 题型:
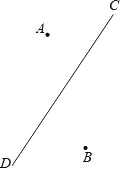
查看答案和解析>>【题目】如图所示,李明和王丽家分别位于公路CD两侧的A,B处,星期天王丽要去为李明送书,他两人约定在公路CD边上见面.李明骑自行车,王丽步行,为节省时间,他们见面的地点定在距离王丽家最近的点E
(1)请你利用所学过的知识,画图确定点E的位置并写出画图依据;
(2)出门前李明发现自行车坏了,临时决定也步行前往,为节省时间,他们约定在距离他两家距离之和最小的F处见面,请你画出图形,确定点F的位置并写出画图依据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体的展开图如图所示,如果正方体的六个面分别用字母A,B,C,D,E,F表示,当各面上的数分别与它对面的数互为相反数,且满足B=1,C=﹣a2﹣2a+1,D=﹣1,E=3a+4,F=2﹣a时,求A面表示的数值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线
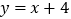 分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.(1)若点P的横坐标为﹣3,当⊙P与x轴相切时,则半径r为 ,此时⊙P与y轴的位置关系是 .(直接写结果)
(2)若
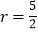 ,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
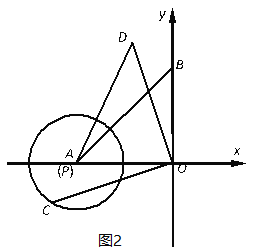
,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.(3)如图2,当圆心P与A重合,
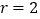 时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.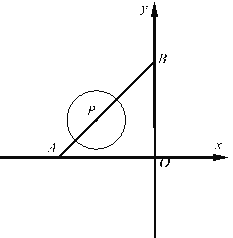
-
科目: 来源: 题型:
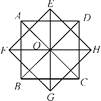
查看答案和解析>>【题目】如图,正方形ABCD与正方形EFGH边长相等,下列说法:
①这个图案可以看成正方形ABCD绕点O旋转45°前后的图形共同组成的;
②这个图案可以看成△ABC绕点O分别旋转45°,90°,135°,180°,225°前后的图形共同组成的;
③这个图案可以看成△BOC绕点O分别旋转45°,90°,135°,225°,250°前后的图形共同组成的.
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 以上都不对
相关试题

