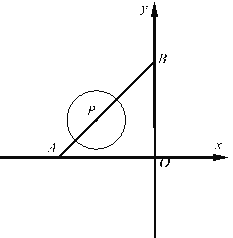
【题目】如图1,直线![]() 分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
分别交x轴、y轴于A、B两点,点P是线段AB上的一动点,以P为圆心,r为半径画圆.
(1)若点P的横坐标为﹣3,当⊙P与x轴相切时,则半径r为 ,此时⊙P与y轴的位置关系是 .(直接写结果)
(2)若![]() ,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
,当⊙P与坐标轴有且只有3个公共点时,求点P的坐标.
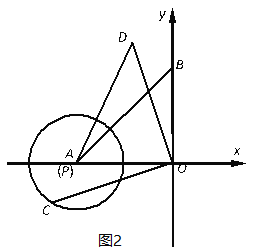
(3)如图2,当圆心P与A重合,![]() 时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
时,设点C为⊙P上的一个动点,连接OC,将线段OC绕点O顺时针旋转90°,得到线段OD,连接AD,求AD长的最值并直接写出对应的点D的坐标.
参考答案:
【答案】(1)![]() ,相离,(2)P
,相离,(2)P![]() 或P
或P![]() ;(3)当点D在线段AB上时,AD最小值为
;(3)当点D在线段AB上时,AD最小值为![]() ,点D坐标为
,点D坐标为![]() ,当点D在线段AB的延长线上时,AD最大值为
,当点D在线段AB的延长线上时,AD最大值为![]() ,点D坐标为
,点D坐标为![]()
【解析】
(1)根据坐标轴上点的坐标特征求出A点和B点的坐标,根据相似三角形的性质解答;
(2)根据直线与圆的位置关系解答;
(3)连接AC,BD,证明△AOC≌△BOD,求出BD的长,得到AD最长或最短距离,根据直角三角形的性质求出点D的坐标.
(1)当x=0时,y=4, 当y=0时,x=-4,
∴A点的坐标为(-4,0),B点的坐标为(0,4),
点N为⊙P与x轴的切点,连接PN,
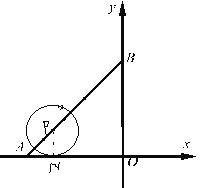
则PN∥OB,
∴![]() ,即
,即![]() ,
,
解得,PN=1,
x+4=1,
解得,x=3,
∵3>1,
∴⊙P与y轴的位置关系是相离,
故答案为:1;相离;
(2)当r=![]() ,⊙P与x轴相切时,
,⊙P与x轴相切时,
由![]() =x+4,得x=
=x+4,得x=![]() ,
,
则⊙P与y轴相交,
此时点P的坐标为(![]() ,
,![]() ),
),
当r=![]() ,⊙P与y轴相切时,
,⊙P与y轴相切时,
由y=![]() +4=
+4=![]() ,
,
则P与x轴相交,
此时点P的坐标为(-![]() ,
,![]() );
);
(3)连接AC、BD,
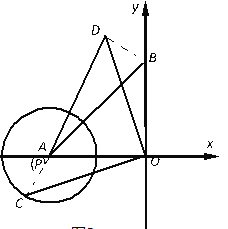
∵∠COD=∠AOB=90°
∴∠COA=∠DOB
易证△AOC≌△BOD
∴BD=AC=2
∴点D的运动轨迹是以点B为圆心,2为半径的圆,
当点D在线段AB上时,AD最小值为![]() ,点D坐标为
,点D坐标为![]() ;
;
当点D在线段AB的延长线上时,AD最大值为![]() ,点D坐标为
,点D坐标为![]() .
.
-
科目: 来源: 题型:
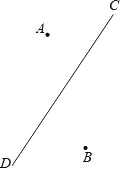
查看答案和解析>>【题目】如图所示,李明和王丽家分别位于公路CD两侧的A,B处,星期天王丽要去为李明送书,他两人约定在公路CD边上见面.李明骑自行车,王丽步行,为节省时间,他们见面的地点定在距离王丽家最近的点E
(1)请你利用所学过的知识,画图确定点E的位置并写出画图依据;
(2)出门前李明发现自行车坏了,临时决定也步行前往,为节省时间,他们约定在距离他两家距离之和最小的F处见面,请你画出图形,确定点F的位置并写出画图依据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
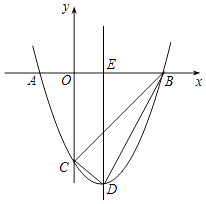
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方体的展开图如图所示,如果正方体的六个面分别用字母A,B,C,D,E,F表示,当各面上的数分别与它对面的数互为相反数,且满足B=1,C=﹣a2﹣2a+1,D=﹣1,E=3a+4,F=2﹣a时,求A面表示的数值.

-
科目: 来源: 题型:
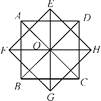
查看答案和解析>>【题目】如图,正方形ABCD与正方形EFGH边长相等,下列说法:
①这个图案可以看成正方形ABCD绕点O旋转45°前后的图形共同组成的;
②这个图案可以看成△ABC绕点O分别旋转45°,90°,135°,180°,225°前后的图形共同组成的;
③这个图案可以看成△BOC绕点O分别旋转45°,90°,135°,225°,250°前后的图形共同组成的.
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究多边形内角和问题.
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.从多边形某一个顶点出发的×对角线可以把一个多边形分成几个三角形.这样就把多边形内角和问题转化为三角形内角和问题了.
(1)请你试一试,做一做,把下面表格补充完整:
名称
图形
内角和
三角形

180°
四边形
2×180°=360°
五边形
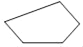
六边形
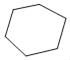
…
…
…
根据表格探究发现的规律,完成下面的问题:
(2)七边形的内角和等于 度;
(3)如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和: .
-
科目: 来源: 题型:
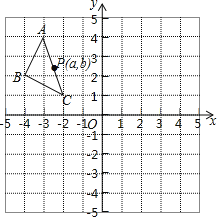
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称。
(1)画出△A1B1C1,并写出点A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对应点为P'(a+3,b+1),请画出平移后的△A2B2C2.
相关试题

