【题目】填空完成推理过程:
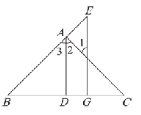
如图,AD⊥BC于点D,EG⊥BC于点G,AD平分∠BA C. 求证: ∠E=∠1.
证明: ∵AD⊥BC于点D,EG⊥BC于点G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义)
∴AD∥EG,( )
∴∠1= ,( )
∠E=∠3,(两直线平行,同位角相等)
∵AD平分∠BAC,(已知)
∴∠2=∠3,( )
∴∠E=∠1.(等量代换)
参考答案:
【答案】同位角相等,两直线平行 , ∠2 ,两直线平行,内错角相等 , 角平分线的定义
【解析】本题根据平行线的判定推出AD∥EG,根据平行线性质得出∠1=∠2,∠3=∠E,根据角平分线定义,推出∠2=∠3,利用等量代换推出∠1=∠E即可.
∵AD⊥BC于点D,EG⊥BC于点G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义)
∴AD∥EG,(同位角相等,两直线平行)
∴∠1=∠2,(两直线平行,内错角相等)
∠E=∠3,(两直线平行,同位角相等)
∵AD平分∠BAC,(已知)
∴∠2=∠3,(角平分线的定义)
∴∠E=∠1.(等量代换)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点 B(m,n) 在第一象限,m,n 均为整数,且满足n =
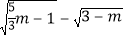 .
.(1) 求点 B 的坐标;
(2) 将线段 OB 向下平移 a 个单位后得到线段 O′B′,过点 B′作 B′C⊥y 轴于点 C,若 3CO=2CO′,求a 的值;
(3) 过点 B 作与 y 轴平行的直线 BM,点 D 在 x 轴上,点 E 在 BM 上,点 D 从 O 点出发以每秒钟 3个单位长度的速度沿 x 轴向右运动,同时点 E 从 B 点出发以每秒钟 2 个单位长度的速度沿BM 向下运动,在点 D,E 运动的过程中,若直线 OE,BD 相交于点 G,且 5≤S△OGB≤10,则点G 的横坐标 xG的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

-
科目: 来源: 题型:
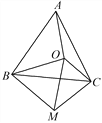
查看答案和解析>>【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个长方形,若它的长增加 9cm,则变为宽的两倍;若它的宽增加 5cm,则只比长少 1cm.
(1) 这个长方形的长和宽各是多少 cm?
(2) 将这个长方形的长减少 a cm,宽增加 b cm,使它变成一个正方形,若 a,b均为正整数,所得正方形的周长不大于原长方形的周长,求这个正方形的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=
 ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
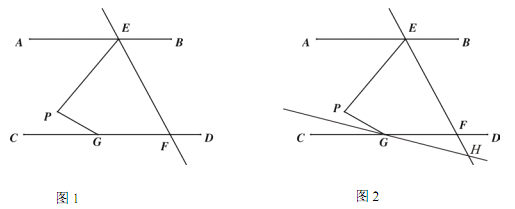
相关试题

