【题目】有一个长方形,若它的长增加 9cm,则变为宽的两倍;若它的宽增加 5cm,则只比长少 1cm.
(1) 这个长方形的长和宽各是多少 cm?
(2) 将这个长方形的长减少 a cm,宽增加 b cm,使它变成一个正方形,若 a,b均为正整数,所得正方形的周长不大于原长方形的周长,求这个正方形的最大面积.
参考答案:
【答案】(1) 长为21cm,宽为15cm ;(2) 324cm2.
【解析】(1)设该长方形的长为![]()
![]() ,宽为
,宽为![]()
![]() ,根据若它的长增加 9cm,则变为宽的两倍和若它的宽增加 5cm,则只比长少 1cm各列一个方程,组成方程组求解即可;
,根据若它的长增加 9cm,则变为宽的两倍和若它的宽增加 5cm,则只比长少 1cm各列一个方程,组成方程组求解即可;
(2)由题意得,![]() ,即
,即![]() ,然后根据a,b均为正整数和所得正方形的周长不大于原长方形的周长列不等式组求解即可.
,然后根据a,b均为正整数和所得正方形的周长不大于原长方形的周长列不等式组求解即可.
(1)设该长方形的长为![]()
![]() ,宽为
,宽为![]()
![]() ,
,
依题意得:![]() ,
,
解得:![]() ,
,
答:该长方形的长为21cm,宽为15cm.
(2)依题意:![]() ,
,
∴![]() ,
,
又 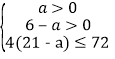 ,
,
∴![]() ,
,
∵ a为整数,所以![]() 3,4,5,
3,4,5,
对应正方形面积分别为324cm2,289cm2,256cm2,
∴这个正方形的最大面积为324cm2.
-
科目: 来源: 题型:
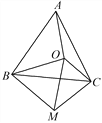
查看答案和解析>>【题目】如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成推理过程:
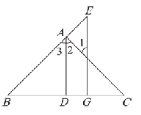
如图,AD⊥BC于点D,EG⊥BC于点G,AD平分∠BA C. 求证: ∠E=∠1.
证明: ∵AD⊥BC于点D,EG⊥BC于点G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义)
∴AD∥EG,( )
∴∠1= ,( )
∠E=∠3,(两直线平行,同位角相等)
∵AD平分∠BAC,(已知)
∴∠2=∠3,( )
∴∠E=∠1.(等量代换)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=
 ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
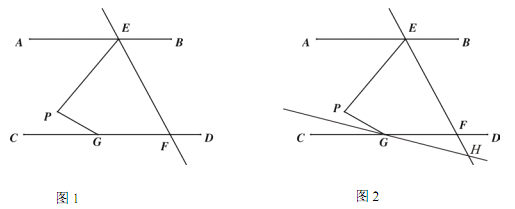
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐篷;
(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
相关试题

