Question

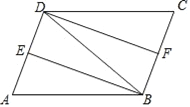
【题目】如图，在ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．

（1）求证：△ABE≌△CDF；

（2）若AB=DB，猜想：四边形DFBE是什么特殊的四边形？并说明理由．

Answer 1

【答案】（1）证明见解析； （2）四边形DFBE是矩形，理由见解析.

【解析】证明：（1）∵四边形ABCD是平行四边形

AB＝CD，∠A＝∠C．

AB∥CD，∴∠ABD＝∠CDB．

∵BE平分∠ABD，DF平分∠CDB，

∴∠ABE＝∠ABD，∠CDF＝∠CDB．

∴∠ABE＝∠CDF．

在△ABE和△CDF中，

∵∠A＝∠C，AB＝CD，∠ABE＝∠CDF，

∴△ABE≌△CDF．

（2）答：四边形DFBE是矩形。理由如下：

∵AB＝DB，BE平分∠ABD

∴BE⊥AD，即∠DEB＝90°．

∵AB＝DB，AB＝CD，∴DB＝CD．

∵DF平分∠CDB，∴DF⊥BC，即∠BFD＝90°．

在□ABCD中，∵AD∥BC，∴∠EDF＋∠DEB＝180°．∴∠EDF＝90°．

∴∠DEB＝∠BFD＝∠EDF＝90°．

∴四边形DFBE是矩形