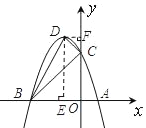
【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)试判断△BCD的形状,并说明理由.

参考答案:
【答案】(1)![]() ,D(﹣1,4); (2) △BCD为直角三角形,理由见解析.
,D(﹣1,4); (2) △BCD为直角三角形,理由见解析.
【解析】试题分析:(1)设抛物线的解析式为y=ax2+bx+c,利用待定系数法求得解析式后,通过配方成顶点式,即可得到顶点坐标;
(2)过点D分别作x轴、y轴的垂线,垂足分别为E、F,在Rt△BOC中,由勾股定理可得BC2 =18,在Rt△CDF中,由勾股定理可得CD2 =2,在Rt△BDE中,由勾股定理可得BD2 =20,从而得BC2+CD2=BD2,由勾股定理的逆定理即可得△BCD为直角三角形.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,
由抛物线与y轴交于点C(0,3),可知c=3,
即抛物线的解析式为y=ax2+bx+3,
把点A(1,0)、点B(﹣3,0)代入,得![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+3,
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点D的坐标为(﹣1,4);
(2)△BCD是直角三角形,理由如下:
过点D分别作x轴、y轴的垂线,垂足分别为E、F,
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18,
在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,
∴CD2=DF2+CF2=2,
在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,
∴BD2=DE2+BE2=20,
∴BC2+CD2=BD2,
∴△BCD为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y1=
 的图象与一次函数y2=
的图象与一次函数y2= 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1= 的图象上.
的图象上.(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中
中 且
且 ,又
,又 、
、 为
为 的三等分点.
的三等分点.
(1)求证
 ;
;(2)证明:
 ;
;(3)若点
 为线段
为线段 上一动点,连接
上一动点,连接 则使线段
则使线段 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由) -
科目: 来源: 题型:
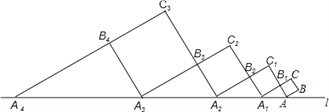
查看答案和解析>>【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
 是关于
是关于 的方程
的方程 的解,求
的解,求 的值.
的值.(2)已知关于x的方程
 的解与方程
的解与方程 的解互为倒数,求
的解互为倒数,求 的值.
的值.(3)小丽在解关于
 的方程
的方程 时,出现了一个失误:“在将
时,出现了一个失误:“在将 移到方程的左边时,忘记了变号.”结果她得到方程的解为
移到方程的左边时,忘记了变号.”结果她得到方程的解为 ,求
,求 的值和原方程的解.
的值和原方程的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用棋子摆成的“上”字.

(1)依照此规律,第4个图形需要黑子、白子各多少枚?
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?
(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

相关试题

