【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=
的图象与一次函数y2=![]() 的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=
的图象交于点A,B,点B的横坐标实数4,点P(1,m)在反比例函数y1=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)观察图象回答:当x为何范围时,y1>y2;
(3)求△PAB的面积.

参考答案:
【答案】(1)反比例函数的表达式为y=![]() ;(2)x<﹣4或0<x<4时,y1>y2;(3)△PAB的面积为15.
;(2)x<﹣4或0<x<4时,y1>y2;(3)△PAB的面积为15.
【解析】
(1)利用一次函数求得B点坐标,然后用待定系数法求得反函数的表达式即可;
(2)观察图象可知,反函数的图象在一次函数图象上方的部分对应的自变量的取值范围就是不等式y1>y2的解;
(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,设AP与y轴交于点C,由点A与点B关于原点对称,得出OA=OB,则S△AOP=S△BOP,即S△PAB=2S△AOP,再求出点P的坐标,利用待定系数法求得直线AP的函数解析式,得到点C的坐标,然后根据S△AOP=S△AOC+S△POC,即可求得结果.
(1)将x=4代入y2=![]() 得:y=1,
得:y=1,
∴B(4,1),
∴k=xy=4×1=4,
∴反比例函数的表达式为y=![]() ;
;
(2)由正比例函数和反比例函数的对称性可知点A的横坐标为﹣4.
∵y1>y2,
∴反比例函数图象位于正比例函数图象上方,
∴x<﹣4或0<x<4;
(3)过点A作AR⊥y轴于R,过点P作PS⊥y轴于S,连接PO,
设AP与y轴交于点C,如图,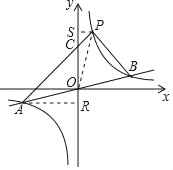
∵点A与点B关于原点对称,
∴OA=OB,
∴S△AOP=S△BOP,
∴S△PAB=2S△AOP,
y1=![]() 中,当x=1时,y=4,
中,当x=1时,y=4,
∴P(1,4),
设直线AP的函数关系式为y=mx+n,
把点A(﹣4,﹣1)、P(1,4)代入y=mx+n,
得![]() ,
,
解得m=3,n=1,
故直线AP的函数关系式为y=x+3,
则点C的坐标(0,3),OC=3,
∴S△AOP=S△AOC+S△POC
=![]() OCAR+
OCAR+![]() OCPS
OCPS
=![]() ×3×4+
×3×4+![]() ×3×1
×3×1
=![]() ,
,
∴S△PAB=2S△AOP=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】10个人围成一圈做游戏.游戏的规则是:每个人心里都想一个数,并把目己想的数告诉与他相邻的两个人,然后每个人将与他相邻的两个人告诉他的数的平均数报出来,若报出来的数如图所示,则报出来的数是3的人心里想的数是( )

A.2B.
 C.4D.
C.4D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则
 的值等于___.
的值等于___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中
中 且
且 ,又
,又 、
、 为
为 的三等分点.
的三等分点.
(1)求证
 ;
;(2)证明:
 ;
;(3)若点
 为线段
为线段 上一动点,连接
上一动点,连接 则使线段
则使线段 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=__.
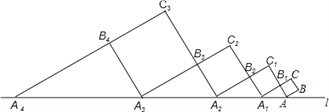
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标;
(2)试判断△BCD的形状,并说明理由.

相关试题

