【题目】如图,已知∠1+∠2=180°,∠DAE=∠BCF.
(1)试判断直线AE与CF有怎样的位置关系?并说明理由;
(2)若∠BCF=70°,求∠ADF的度数.
参考答案:
【答案】
(1)解:AE∥CF,
理由是:∵∠1+∠2=180°,∠BDC+∠2=180°,
∴∠1=∠BDC,
∴AE∥CF;
(2)解:∵AE∥CF,
∴∠BCF=∠CBE,
又∵∠DAE=∠BCF,
∴∠DAE=∠CBE,
∴AD∥BC,
∴∠ADF=∠BCF=70°.
【解析】(1)根据图形可知∠BDC+∠2=180°或∠DBC+∠1=180°,结合已知,根据同角的余角相等,得出∠1=∠BDC或∠DBC=∠2证得结论。
(2)先根据已知证明∠DAE=∠CBE,再根据平行线的判定得出AD∥BC,然后根据两直线平行同位角相等,即可求出结果。
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )

A. BD=CE B. AD=AE C. DA=DE D. BE=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合.
(1)直尺的长为多少个单位长度(直接写答案)
(2)如图2,直尺AB在数轴上移动,有BC=4OA,求此时A点对应的数;
(3)如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2, 若t1﹣t2=2(秒),求直尺放入蓬内,A点对应的数为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x
﹣3
﹣2
﹣1
0
1
2
3
4
5
y
12
5
0
﹣3
﹣4
﹣3
0
5
12
给出了结论:
⑴二次函数y=ax2+bx+c有最小值,最小值为﹣3;
⑵当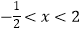 时,y<0;
时,y<0;
⑶二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.则其中正确结论的个数是( )
A.3
B.2
C.1
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三个边长分别为2,3,5的三个菱形如图排列,菱形的较小锐角为60°,则图中阴影部分的面积为( )
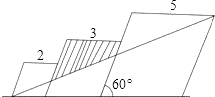
A.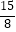
B.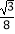
C.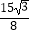
D.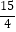
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
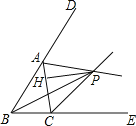
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.

相关试题

