【题目】已知,一个点从数轴上的原点开始,先向左移动7cm到达A点,再从A点向右移动12cm到达B点,把点A到点B的距离记为AB,点C是线段AB的中点.
(1)点C表示的数是_____;
(2)若点A以每秒2cm的速度向左移动,同时C、B点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,
①点C表示的数是_____(用含有t的代数式表示);
②当t=2秒时,求CB﹣AC的值;
③试探索:CB﹣AC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
参考答案:
【答案】(1)﹣1 0
【解析】
(1)由题意得A点表示的数为﹣7,B点表示的数为5,求出AB的长度,进而求出AC的长度,即可求出点C表示的数;(2)①用含t的代数式表示出C点即可;②分别求出t=2时CB、AC的长度,进而求出CB﹣AC的值;③用含t的式子分别表示出A、B、C三个点,进而表示出CB、AC的长度,计算出CB﹣AC的值即可判断是否变化.
(1)由题意可得:A点表示的数为﹣7,B点表示的数为5,
∴AB=12,
∴AC=12×![]() =6,
=6,
∴点C表示的数为:﹣7+6=﹣1,
故答案为:﹣1;
(2)①由题意可得,
点C移动t秒时表示的数为:﹣1+t,
故答案为:﹣1+t;
②当t=2时,A点表示的数为﹣7﹣2×2=﹣11,
B点表示的数为5+4×2=13,
C点表示的数为﹣1+1×2=1,
∴CB=12,AC=12,
∴CB﹣AC=0;
③CB﹣AC的值不随着时间t的变化而改变,
A点表示的数为﹣7﹣2t,
B点表示的数为5+4t,
C点表示的数为﹣1+t,
∴CB=5+4t﹣(﹣1+t)=6+3t,
AC=﹣1+t﹣(﹣7﹣2t)=6+3t,
∴CB﹣AC=0,
∴CB﹣AC的值不随着时间t的变化而改变,CB﹣AC的值为0cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在平面直角坐标系中,A(-1,-3),OB=
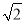 ,OB与x轴所夹锐角是45°
,OB与x轴所夹锐角是45°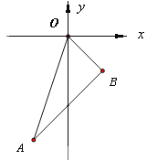
(1)求B点坐标
(2)判断三角形ABO的形状
(3)求三角形ABO的AO边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)﹣7+13﹣6+20;
(2)3+(﹣2)﹣3×(﹣5)×0;
(3)16÷(﹣2)3﹣(﹣
 )×(﹣4);
)×(﹣4);(4)﹣36×(
 );
);(5)(2a2﹣1+2a)﹣(a﹣1+a2);
(6)8a+2b﹣2(5a﹣2b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技开发公司研制出一种新型的产品,每件产品的成本为2400元,销售单价定为3000元,在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获得的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获得的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC.
(1)如图①,P为等边△ABC外一点,且∠BPC=120°,试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
(2)如图②,P为等边△ABC内一点,且∠APD=120°,求证:PA+PD+PC>BD;
(3)在(2)的条件下,若∠CPD=30°,AP=4,CP=5,DP=8,求BD的长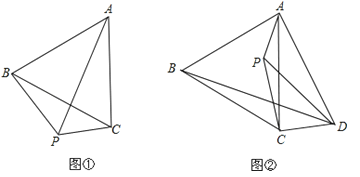
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
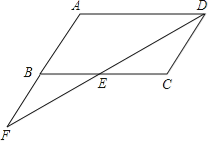
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号
1
2
3
4
5
6
正方形个数
1
4
7
10
_____
_____
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?
相关试题

