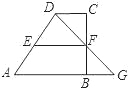
【题目】如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:△CDF∽△BGF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.
参考答案:
【答案】(1)证明见解析(2)CD=2cm
【解析】
试题分析:(1)利用平行线的性质可证明△CDF∽△BGF.
(2)根据点F是BC的中点这一已知条件,可得△CDF≌△BGF,则CD=BG,只要求出BG的长即可解题.
试题解析:(1)∵梯形ABCD,AB∥CD,
∴∠CDF=∠G,∠DCF=∠GBF,
∴△CDF∽△BGF.
(2)由(1)△CDF∽△BGF,
又∵F是BC的中点,BF=FC,
∴△CDF≌△BGF,
∴DF=GF,CD=BG,
∵AB∥DC∥EF,F为BC中点,
∴E为AD中点,
∴EF是△DAG的中位线,
∴2EF=AG=AB+BG.
∴BG=2EF﹣AB=2×4﹣6=2,
∴CD=BG=2cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015“五一”长假,波月洞景区授待游客约110000人次,将110000用科学记数法表示为( )
A.11×104
B.1.1×105
C.1.1×106
D.11万 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列不等式一定成立的是( )
A. 1-a<1-b B. -a>-b C. ac2>bc2 D. a-2<b-2
-
科目: 来源: 题型:
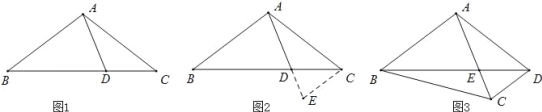
查看答案和解析>>【题目】阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为 ,AC的长为 .
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-1,2)关于y轴对称的点的坐标是( )
A. (1,2) B. (-1,2) C. (1,-2) D. (-1,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为__________个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

