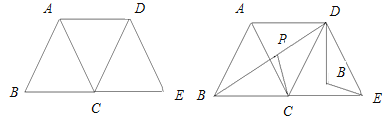
【题目】已知三个全等的等边三角形如图1所示放置,其中点B、C、E在同一直线上,
(1)写出两个不同类型的结论;
(2)连接BD,P为BD上的动点(D点除外),DP绕点D逆时针旋转60到DQ,如图2,连接PC,QE,
①判断CP与QE的大小关系,并说明理由;
②若等边三角形的边长为2,连接AP,在BD上是否存在点P,使AP+CP+DP的值最小,并求最小值.
参考答案:
【答案】(1)答案见解析;(2)①CP=QE,理由见解析;②存在,AP+CP+DP的最小值为![]()
【解析】解:(1)答案不唯一,合理即可,
如AD∥BE,四边形ABCD、ACED是菱形;
四边形ABED是等腰梯形;四边形ABED是轴对称图形;
 (2)①CP=QE;理由:
(2)①CP=QE;理由:
∵△AEC是等边三角形,
∴CD=DE,∠CDE=60,
∵DP绕点D逆时针旋转60到DQ,
∴PD=DQ,∠PDQ=60,
∴∠PDQ=∠QDE,
∴△DPC≌△DQE
∴CP=QE。
②连接AP,由①可知CP=QE,
∵DP绕点D逆时针旋转60到DQ,
∴△DPQ是等边三角形,
∴DP=DQ,
要使AP+CP+DP的值最小,关键是AP+QE+QP的值最小,即点A、P、Q、E在同一直线上(AE),构建两点之间,线段最短,过点A作AM⊥BE于点M,可得BM=1,EM=3,AM=![]() ,
,
所以AE=![]() ,
,
故在BD上存在点P,故AP+CP+DP的值最小,最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A.y=﹣3x+2
B.y=﹣3x﹣2
C.y=﹣3(x+2)
D.y=﹣3(x﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C在线段AD上,CD=2AB+3.
(1)若点C是线段AD的中点,求BC-AB的值;
(2)若BC=
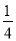 AD,求BC-AB的值;
AD,求BC-AB的值;(3)若线段AC上有一点P(不与点B重合),AP+AC=DP,求BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+a)(x+b)=x2﹣x-12,则a,b的值可能分别是( )
A. ﹣3,﹣4B. ﹣3,4C. 3,﹣4D. 3,4
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C在x轴上方,y轴左侧,距离x轴2个单位,距离y轴3个单位,则点C的坐标为( )
A. (2,3) B. (-2,-3) C. (-3,2) D. (3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2m(3m﹣5)+3m(1﹣2m)=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
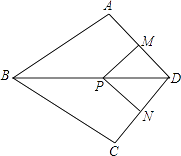
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
相关试题

