【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 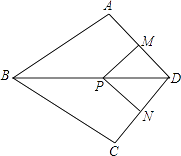
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
参考答案:
【答案】
(1)证明:∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
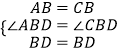 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB
(2)证明:∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.
【解析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
【考点精析】根据题目的已知条件,利用正方形的判定方法的相关知识可以得到问题的答案,需要掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.
-
科目: 来源: 题型:
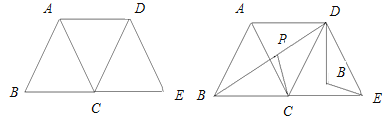
查看答案和解析>>【题目】已知三个全等的等边三角形如图1所示放置,其中点B、C、E在同一直线上,
(1)写出两个不同类型的结论;
(2)连接BD,P为BD上的动点(D点除外),DP绕点D逆时针旋转60到DQ,如图2,连接PC,QE,
①判断CP与QE的大小关系,并说明理由;
②若等边三角形的边长为2,连接AP,在BD上是否存在点P,使AP+CP+DP的值最小,并求最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C在x轴上方,y轴左侧,距离x轴2个单位,距离y轴3个单位,则点C的坐标为( )
A. (2,3) B. (-2,-3) C. (-3,2) D. (3,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2m(3m﹣5)+3m(1﹣2m)=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国“钓鱼岛”周围海域面积约170 000km2 , 该数用科学记数法可表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+y)2=25,则x+y 的值为( )
A. 10,B. 5,C. -5,D. ±5
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:5x(x+1)=2(x+1)
相关试题

