【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣3,3).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
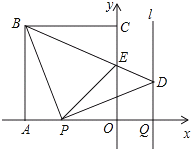
(1)求∠EBP的度数;
(2)求点D运动路径的长;
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
参考答案:
【答案】(1)∠PBD =45°.
(2)点D运动路径的长为t;
(3)△POE周长是定值,该定值为6.
【解析】
试题分析:(1)易证△BAP≌△PQD,从而得到BP=PD,由∠BPD=90°,从而可以求出∠PBE的度数;
(2)由△BAP≌△PQD,从而得到DQ=AP=t;
(2)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.容易得到△POE周长等于AO+CO=8,从而解决问题;
解:(1)如图,由题可得:AP=OQ=1×t=t(秒)
∴AO=PQ
∵四边形OABC是正方形,
∴AO=AB=BC=OC,
∠BAO=∠AOC=∠OCB=∠ABC=90°.
∵DP⊥BP,
∴∠BPD=90°.
∴∠BPA=90°﹣∠DPQ=∠PDQ.
∵AO=PQ,AO=AB,
∴AB=PQ.
在△BAP和△PQD中,
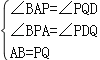
∴△BAP≌△PQD(AAS).
∴BP=PD.
∵∠BPD=90°,BP=PD,
∴∠PBD=∠PDB=45°.
(2)∵△BAP≌△PQD,
∴DQ=AP,
∵AP=t,
∴DQ=t.
∴点D运动路径的长为t;
(3)∵∠EBP=45°
∴由图1可以得到EP=CE+AP,
∴OP+PE+OE=OP+AP+CE+OE
=AO+CO
=3+3
=6.
∴△POE周长是定值,该定值为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AD=8,
 ABC=1200,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为_________.
ABC=1200,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为_________.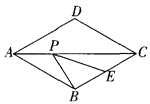
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示,请解答下列问题:
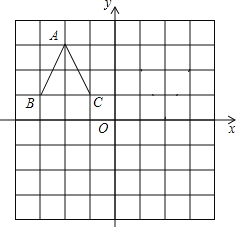
(1)将△ABC向下平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;
(2)将△ABC绕点O顺时针方向旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2,并写出A2点的坐标.
-
科目: 来源: 题型:
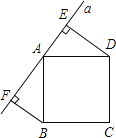
查看答案和解析>>【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形分别为绿色食品、节能、节水、回收的标志图片,其中是中心对称图形或者是轴对称图形的为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣5x﹣6=0.
相关试题

