【题目】如图,抛物线y=a(x﹣h)2+k经过点A(0,1),且顶点坐标为B(1,2),它的对称轴与x轴交于点C.
(1)求此抛物线的解析式.
(2)在第一象限内的抛物线上求点P,使得△ACP是以AC为底的等腰三角形,请求出此时点P的坐标.
(3)上述点是否是第一象限内此抛物线上与AC距离最远的点?若是,请说明理由;若不是,请求出第一象限内此抛物线上与AC距离最远的点的坐标.
参考答案:
【答案】
(1)
解:∵抛物线y=a(x﹣h)2+k顶点坐标为B(1,2),
∴y=a(x﹣1)2+2,
∵抛物线经过点A(0,1),
∴a(0﹣1)2+2=1,
∴a=﹣1,
∴此抛物线的解析式为y=﹣(x﹣1)2+2或y=﹣x2+2x+1;
(2)
解:∵A(0,1),C(1,0),
∴OA=OC,
∴△OAC是等腰直角三角形.
过点O作AC的垂线l,根据等腰三角形的“三线合一”的性质知:l是AC的中垂线,
∴l与抛物线的交点即为点P.
如图,直线l的解析式为y=x,
解方程组 ![]() ,
,
得  ,
,  (不合题意舍去),
(不合题意舍去),
∴点P的坐标为( ![]() ,
, ![]() );
);
(3)
解:点P不是第一象限内此抛物线上与AC距离最远的点.
由(1)知,点C的坐标为(1,0).
设直线AC的解析式为y=kx+b,
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣x+1.
设与AC平行的直线的解析式为y=﹣x+m.
解方程组 ![]() ,
,
代入消元,得﹣x2+2x+1=﹣x+m,
∵此点与AC距离最远,
∴直线y=﹣x+m与抛物线有且只有一个交点,
即方程﹣x2+2x+1=﹣x+m有两个相等的实数根.
整理方程得:x2﹣3x+m﹣1=0,
△=9﹣4(m﹣1)=0,解之得m= ![]() .
.
则x2﹣3x+ ![]() ﹣1=0,解之得x1=x2=
﹣1=0,解之得x1=x2= ![]() ,此时y=
,此时y= ![]() .
.
∴第一象限内此抛物线上与AC距离最远的点的坐标为( ![]() ,
, ![]() ).
).
【解析】(1)由抛物线y=a(x﹣h)2+k的顶点坐标是B(1,2)知:h=1,k=2,则y=a(x﹣1)2+2,再把A点坐标代入此解析式即可;(2)易知△OAC是等腰直角三角形,可得AC的垂直平分线是直线y=x,根据“线段垂直平分线上的点到线段两个端点的距离相等”知直线y=x与抛物线的交点即为点P,解方程组即可求出P点坐标;(3)先求出第一象限内此抛物线上与AC距离最远的点的坐标,再与P点的坐标比较进行判断.满足条件的点一定是与直线AC平行且与抛物线有唯一交点的直线与抛物线相交产生的,易求出直线AC的解析式,设出与AC平行的直线的解析式,令它与抛物线的解析式组成的方程组有唯一解,求出交点坐标,通过判断它与点P是否重合来判断点P是否是第一象限内此抛物线上与AC距离最远的点.
-
科目: 来源: 题型:
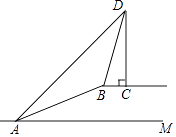
查看答案和解析>>【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈
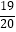 ,cos73°≈0.
,cos73°≈0. 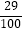 ,tan73°≈
,tan73°≈ 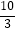 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用y=
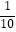 x2﹣
x2﹣ 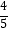 x+3表示
x+3表示 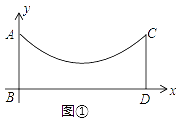
(1)求这条绳子最低点离地面的距离;
(2)现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑(如图②),已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.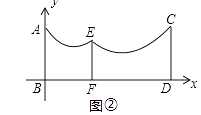
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是CD的中点,AE是延长线交BC的延长线于F,分别连接AC,DF,解答下列问题:
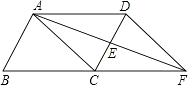
(1)求证:△ADE≌△FCE;
(2)若DC平分∠ADF,试确定四边形ACFD是什么特殊四边形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交与点P,BE与CD交于点Q,连接PQ.
求证:(1)AD=BE
(2)△APC≌△BQC
(3)△PCQ是等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.5﹣1=
B.x2?x3=x6
C.(a+b)2=a2+b2
D.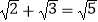
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市举行的中学生安全知识竞赛中共有20道题.每一题答对得5分,答错或不答都扣3分.
(1)小李考了60分,那么小李答对了多少道题?
(2)小王获得二等奖(75~85分),请你算算小王答对了几道题?
相关试题

