【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连接CC′,则∠CC′B′的度数是( ) 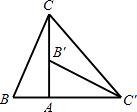
A.45°
B.30°
C.25°
D.15°
参考答案:
【答案】D
【解析】解:由旋转的性质可知,AC=AC′, 又∠CAC′=90°,可知△CAC′为等腰直角三角形,
所以,∠CC′A=45°.
∵∠CC′B′+∠ACC′=∠AB′C′=∠B=60°,
∴∠CC′B′=15°.
故选D.
【考点精析】利用旋转的性质对题目进行判断即可得到答案,需要熟知①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
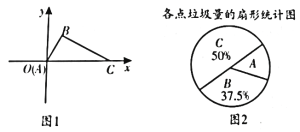
查看答案和解析>>【题目】2017年4月20日,成都举行了“建城市森林,享低碳生活”的垃圾分类推进工作启动仪式,在成都设置有专门的垃圾存放点,做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示,点A在原点,
 ,
, .某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
.某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。(1)若C处的垃圾存放量为320千克,求A处的垃圾存放量。
(2)现需要A,C两处的垃圾分别沿道路AB,CB都运到B处,若点B的横坐标为50,平面直角坐标系中一个单位长度所表示的实际距离是1米,每运送1千克垃圾1米的费用为0.005元,求本次运送垃圾的总费用。(结果保留整数,参考数据:
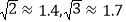 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为
 ,并说明理由.
,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.

(1)①填空:△ACE∽∽;
(2)求证:△CDE∽△CBA;
(3)求证:△FBD≌△EDC;
(4)若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )
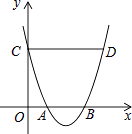
A.2
B.1
C.3
D.1.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为 .
相关试题

