【题目】如图,在△ABC中,点D在△ABC的内部且DB=DC,点E,F在△ABC的外部,FB=FA,EA=EC,∠FBA=∠DBC=∠ECA.
(1)①填空:△ACE∽∽;
(2)求证:△CDE∽△CBA;
(3)求证:△FBD≌△EDC;
(4)若点D在∠BAC的平分线上,判断四边形AFDE的形状,并说明理由.
参考答案:
【答案】
(1)△ABF;△BCD
(2)
解:由①知,△ACE∽△BCD,
∴ ![]() ,即
,即 ![]() ,
,
∵∠ECA=∠DCB,
∴∠ECD=∠ACB,
∴△CDE∽△CBA
(3)
证明:∵△CDE∽△CBA,
∴∠ABC=∠EDC,
∵∠ABC=∠FBD,
∴∠EDC=∠FBD,
同理△BFD∽△BAC,
∴∠FDB=∠ACB,
∵∠ACB=∠ECD,
∴∠FDB=∠ACB,
在△FBD与△EDC中 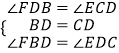 ,
,
∴△FBD≌△EDC;
(4)
解:四边形AFDE是菱形,
理由:∵△FBD≌△EDC,
∴FB=DE,DF=CE,
∵FB=FA,EA=EC,
∴FD=AE,FA=DE,
∴四边形AFDE是平行四边形,
连接AD,则AD平分∠BAC,
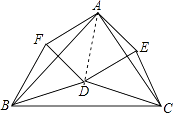
即∠BAD=∠CAD,
∵∠BAF=∠CAE,
∴∠DAF=∠DAE,
∵AF∥DE,
∴∠DAF=∠ADE,
∴∠EAD=∠ADE,
∴EA=ED,
∴AFDE是菱形.
【解析】解:(1)∵DB=DC,
∴∠DBC=∠DCB,
∵FB=FA,EA=EC,
∴∠FBA=∠FAB,∠ACE=∠EAC,
∵∠FBA=∠DBC=∠ECA,
∴∠FAB=∠BCD=∠EAC,
∴△ACE∽△ABF∽△BCD;
故答案为:△ABF,△BCD;
(1)根据等腰三角形的性质得到∠DBC=∠DCB,∠FBA=∠FAB,∠ACE=∠EAC,等量代换得到∠FAB=∠BCD=∠EAC,于是得到结论;(2)根据相似三角形的性质得到 ![]() ,根据相似三角形的判定定理即可得到结论;(3)根据相似三角形的性质得到∠EDC=∠FBD,∠FDB=∠ACB等量代换得到∠FDB=∠ACB,根据全等三角形的判定即可得到结论;(4)根据全等三角形的性质得到FB=DE,DF=CE,等量代换得到FD=AE,FA=DE,推出四边形AFDE是平行四边形,连接AD,于是得到AD平分∠BAC,根据菱形的判定定理即可得到结论.
,根据相似三角形的判定定理即可得到结论;(3)根据相似三角形的性质得到∠EDC=∠FBD,∠FDB=∠ACB等量代换得到∠FDB=∠ACB,根据全等三角形的判定即可得到结论;(4)根据全等三角形的性质得到FB=DE,DF=CE,等量代换得到FD=AE,FA=DE,推出四边形AFDE是平行四边形,连接AD,于是得到AD平分∠BAC,根据菱形的判定定理即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=
 (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.

(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是 .
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游风景区出售一种纪念品,该纪念品的成本为12元/个,这种纪念品的销售价格为x(元/个)与每天的销售数量y(个)之间的函数关系如图所示.

(1)求y与x之间的函数关系式;
(2)销售价格定为多少时,每天可以获得最大利润?并求出最大利润.
(3)“十一”期间,游客数量大幅增加,若按八折促销该纪念品,预计每天的销售数量可增加200%,为获得最大利润,“十一”假期该纪念品打八折后售价为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组﹣2≤x+1<1的解集,在数轴上表示正确的是( )
A.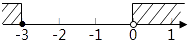
B.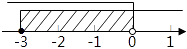
C.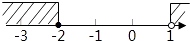
D.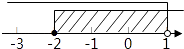
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是( )
A.正比例函数
B.一次函数
C.反比例函数
D.二次函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( )

A.
B.
C.
D.
相关试题

