Question

【题目】如图，已知，现将直角三角形放入图中，其中，交于点，交于点．

（1）当直角三角形所放位置如图①所示时，与存在怎样的数量关系?请说明理由．

（2）当直角三角形所放位置如图②所示时，请直接写出与之间存在的数量关系．

（3）在（2）的条件下，若与交于点，且，则的度数为．

Answer 1

【答案】（1）∠PFD+∠AEM=90°，理由见解析；（2）∠PFD﹣∠AEM=90°；（3）30°．

【解析】

（1）延长MP，交CD于点H，根据AB∥CD得到∠1=∠AEM ，因为∠NPM=90°等量代换即可得出结论，

（2）由题意知：∠AEM=∠PEH，∠PHE=∠BHF，得到∠AEM+∠BHF=90°，再由AB∥CD得到∠PFD+∠BHF=180°，根据等式性质代入即可，

（3）作MQ∥CD，根据AB∥CD∥MQ得∠AEM=∠PMQ，∠QMN=∠MOC，等量代换即可求解．

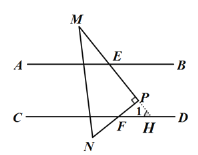
（1）∠PFD+∠AEM=90°，

延长MP，交CD于点H，

∵AB∥CD，

∴∠1=∠AEM ，

∵∠NPM=90°，

∴∠FPH=180°﹣∠NPM=90°，

∵∠1＋∠PFD＋∠FPH=180°，

∴∠1＋∠PFD=90°，

∴∠PFD+∠AEM=90°；

（2）如图：

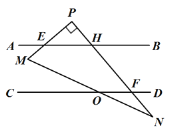
∠PFD﹣∠AEM=90°，

由题意知：∠AEM=∠PEH，∠PHE=∠BHF，

∵∠PEH+∠PHE=90°，

∴∠AEM+∠BHF=90°，

又AB∥CD，

∴∠PFD+∠BHF=180°，

∴∠PFD+∠BHF-（∠AEM+∠BHF）=180°-90°

即∠PFD﹣∠AEM=90°，

（3）30°

作MQ∥CD，

∵AB∥CD，

∴AB∥CD∥MQ，

∴∠AEM=∠PMQ，∠QMN=∠MOC，

∵，∠DON=∠MOC，

∴∠PMQ=40°，∠QMN=20°，

∴∠PMN=60°，

又∠P=90°，

∴∠N=90°-60°=30°．