【题目】如图,利用标杆BE测量建筑物的高度,如果标杆BE长1.2m,测得AB=1.6m,BC=8.4m,楼高CD是多少?
参考答案:
【答案】解:解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴ ![]() ,
,
∵BE=1.2,AB=1.6,BC=8.4,
∴AC=10,
∴ ![]() ,
,
∴CD=7.5.
答:楼高CD是7.5m.
【解析】先根据题意得出△ABE∽△ACD,再根据相似三角形的对应边成比例即可求出CD的值.
【考点精析】根据题目的已知条件,利用相似三角形的应用的相关知识可以得到问题的答案,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.

(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3 . C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按
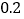 元
元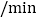 计;B类收费标准如下:没有月租费,但通话费按
计;B类收费标准如下:没有月租费,但通话费按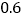 元
元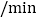 计
计 按照此类收费标准完成下列各题:
按照此类收费标准完成下列各题: 直接写出每月应缴费用
直接写出每月应缴费用 元
元 与通话时长
与通话时长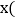 分
分 之间的关系式:
之间的关系式:A类:______B类:______
 若每月平均通话时长为300分钟,选择______类收费方式较少.
若每月平均通话时长为300分钟,选择______类收费方式较少. 求每月通话多长时间时,按
求每月通话多长时间时,按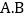 两类收费标准缴费,所缴话费相等.
两类收费标准缴费,所缴话费相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线c和直线b相较于点
 ,直线c过点
,直线c过点 平行于y轴的动直线a的解析式为
平行于y轴的动直线a的解析式为 ,且动直线a分别交直线b、c于点D、
,且动直线a分别交直线b、c于点D、 在D的上方
在D的上方 .
. 求直线b和直线c的解析式;
求直线b和直线c的解析式; 若P是y轴上一个动点,且满足
若P是y轴上一个动点,且满足 是等腰直角三角形,求点P的坐标.
是等腰直角三角形,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )

A. 10cm B. 12cm C. 15cm D. 17cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,现将直角三角形
,现将直角三角形 放入图中,其中
放入图中,其中 ,
, 交
交 于点
于点 ,
, 交
交 于点
于点 .
.

(1)当直角三角形
 所放位置如图①所示时,
所放位置如图①所示时, 与
与 存在怎样的数量关系?请说明理由.
存在怎样的数量关系?请说明理由.(2)当直角三角形
 所放位置如图②所示时,请直接写出
所放位置如图②所示时,请直接写出 与
与 之间存在的数量关系.
之间存在的数量关系.(3)在(2)的条件下,若
 与
与 交于点
交于点 ,且
,且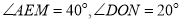 ,则
,则 的度数为.
的度数为.
相关试题

