【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( ) 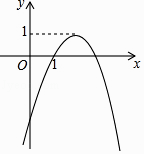
A.a<0,b<0,c>0
B.﹣ ![]() =1
=1
C.a+b+c<0
D.关于x的方程x2+bx+c=﹣1有两个不相等的实数根
参考答案:
【答案】D
【解析】解:A、错误.a<0,b>0,c<0. B、错误.﹣ ![]() >1.
>1.
C、错误.x=1时,y=a+b+c=0.
D、正确.观察图象可知抛物线y=ax2+bx+c与直线y=﹣1有两个交点,所以关于x的方程x2+bx+c=﹣1有两个不相等的实数根.
故选D.
【考点精析】本题主要考查了求根公式和二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠AOB=100°,∠BOD=60°,∠AOC=70°时,则∠COD=_____°(自己画图并计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间
(小时)2
2.5
3
3.5
4
学生人数(名)
1
2
8
6
3
则关于这20名学生阅读小时数的说法正确的是( )
A.众数是8
B.中位数是3
C.平均数是3
D.方差是0.34 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)判断△BEC的形状,并说明理由?
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;
(3)求四边形EFPH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 的解析表达式为:y=-3x+3,且
的解析表达式为:y=-3x+3,且 与x轴交于点D,直线
与x轴交于点D,直线 经过点A,B,直线
经过点A,B,直线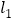 ,
,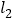 交于点C.
交于点C.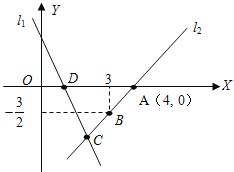
(1)求点D的坐标;
(2)求直线
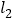 的解析表达式;
的解析表达式;(3)求△ADC的面积;
(4)在直线
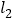 上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP的面积是△ADC面积的2倍,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB=
 ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为 .
.【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=
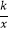 (k≠0)的图象恰好经过点C和点D,则k的值为( )
(k≠0)的图象恰好经过点C和点D,则k的值为( ) 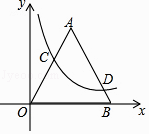
A.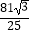
B.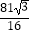
C.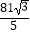
D.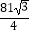
相关试题

