搜索
【题目】如图,在△ABC 中，AB=AC,∠BAC 的角平分线与∠ABC 的角平分线交于点 D,若∠ADB=130°，∠C=（ ）
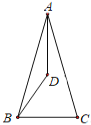
A.50°B.65°C.80°D.100°
参考答案：
【答案】C
【解析】
本题考察的是角平分线的定义与三角形内角和的运用，由三角形内角和为180°，∠ADB=130°可知，∠DAB与∠DBA的和，再由角平分线的定义可知，∠CAB与∠CBA的和，再利用三角形内角和为180°可求∠C
∵在△ABD中，∠ADB=130°，∴∠DAB+∠DBA=180°-∠ADB=50°，又∵DA与DB分别是∠ABC与∠BAC 的角平分线，∴∠CAB+∠CBA=2（∠DAB+∠DBA）=100°，∴∠C=180°-（∠CAB+∠CBA）=80°
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列图形都是由同样大小的黑点按一定的规律组成，摆第1个图案需要4个圆点，摆第2个图案需要7个圆点，摆第3个图案需要10个圆点，摆第4个图案需要13个圆点，按照这个规律继续摆放，第12个图摆放圆点的个数为（ ）
A.21B.35C.37D.43
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，∠OCD＝60°，连接OD．
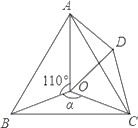
（1）求证：△OCD是等边三角形；
（2）当α＝150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时，△AOD是等腰三角形．
-
科目： 来源： 题型：
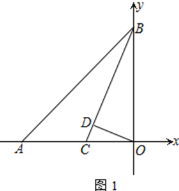
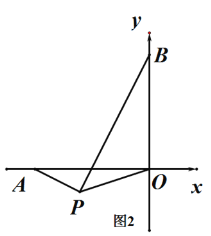
查看答案和解析>>【题目】如图，A(－t，0)、B(0，t)，其中t＞0，点C为OA上一点，OD⊥BC于点D，且∠BCO=45°＋∠COD
(1) 求证：BC平分∠ABO
(2) 求
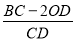的值(3) 若点P为第三象限内一动点，且∠APO=135°，试问AP和BP是否存在某种确定的位置关系？说明理由
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两小朋友都从
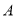地出发，匀速步行到
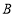地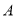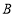（、两地之间为笔直的道路）甲出发半分钟后，乙才从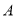地出发，经过一段时间追上甲，两人继续向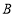地步行，当甲、乙之间的距离刚好是70米时，乙立刻掉头以原速度向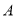地步行，半分钟后与甲相遇，乙又立刻掉头向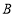地以原速度步行（两次掉头时间忽略不计）．甲、乙相距的路程为
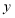（米）与乙出发的时
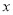（分钟）之间的关系如图所示，当乙到达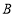地时，甲与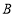地相距的路程是__________米．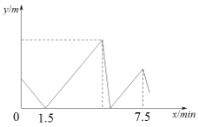
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的盒子里，装有四个分别标有数字1、2、3、4的小球，它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球，记下数字为x；放回盒子摇匀后，再由小华随机抽取一个小球，记下数字为y.则小明、小华各取一次小球所确定的数x，y满足y<
的概率是（ ）A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】新型冠状病毒爆发，教育部部署了“停课不停学”的有关工作，各地都在进行在线教育．小依同学为了了解网课学习情况，对本班部分同学最喜爱的课程进行了调查，调查课程分别是网上授课、体育锻炼、名著阅读、艺术欣赏和其他课程并制成以下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：
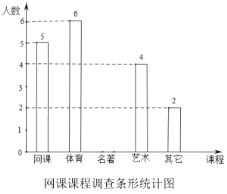
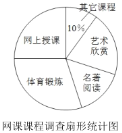
（1）本次调查中一共调查了__________名学生，其中“名著阅读”所占的圆心角度数为__________．
（2）请把条形统计图补全．
（3）在调查的同学中随机选取一名学生，求他恰好最喜爱的课程是“艺术欣赏”的概率．
（4）若该校一共有3000名学生，请估算出全校最喜爱的课程是“体育锻炼”的人数．
相关试题
