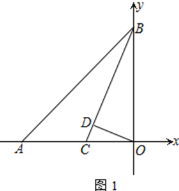
【题目】如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC于点D,且∠BCO=45°+∠COD
(1) 求证:BC平分∠ABO
(2) 求![]() 的值
的值
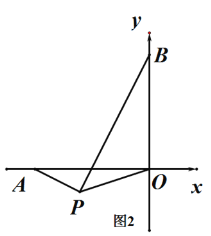
(3) 若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由
参考答案:
【答案】(1)见解析;(2)2;(3)BP⊥AP,理由见解析;
【解析】
(1)分别证明:∠ABC=∠DOC,∠CBO=∠DOC即可.
(2)在BC上截DE=DO,证CE=OE=BE,则E为BC的中点,则BC=2EC=2(DE+DC)=2(OD+CD),代入化简即可,也可以用四点共圆去思考更加简单.
(3)作OM⊥OP交PB于M,交AP的延长线于N,在证明△BOP≌△AON,即可解答.
(1)证明:如图1中,∵AO=BO=t,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵∠BCO=45°+∠COD=∠BAO+∠ABC,
∴∠COD=∠ABC,
∵OD⊥BC,
∴∠CDO=90°,
∵∠DOC+∠DCO=90°,∠CBO+∠BCO=90°,
∴∠DOC=∠CBO,
∴∠ABC=∠CBO.
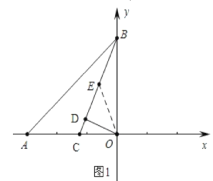
(2)中图1中,作DE=DO,
∵∠ODE=90°,
∴∠DEO=45°=∠EBO+∠EOB,
∵∠ABC=∠CBO=![]() ∠ABO=22.5°,
∠ABO=22.5°,
∴∠EOB=∠EBO=22.5°,
∴EB=EO,
∵∠ECO=∠EOC=67.5°,
∴EC=EO,
∴BC=2EC=2(DE+CD)=2OD+2CD,
∴![]() =2.
=2.
(3)结论:BP⊥AP,如图2,理由如下:
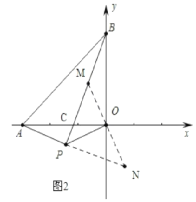
作OM⊥OP交PB于M,交AP的延长线于N,
∵∠APO=135°,
∴∠OPN=∠N=45°,
∴OP=ON,
∵∠AOB=∠PON=90°,
∴∠BOP=∠AON,
在△OBP和△OAN中,
 ,
,
∴△BOP≌△AON,
∴∠BPO=∠N=45°,
∵∠OPN=45°,
∴∠BPN=∠BPO+∠OPN=90°,
∴BP⊥AP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由同样大小的黑点按一定的规律组成,摆第1个图案需要4个圆点,摆第2个图案需要7个圆点,摆第3个图案需要10个圆点,摆第4个图案需要13个圆点,按照这个规律继续摆放,第12个图摆放圆点的个数为( )




A.21B.35C.37D.43
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
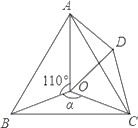
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,∠BAC 的角平分线与∠ABC 的角平分线交于点 D,若∠ADB=130°,∠C=( )
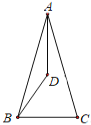
A.50°B.65°C.80°D.100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两小朋友都从
 地出发,匀速步行到
地出发,匀速步行到 地(
地(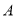 、
、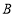 两地之间为笔直的道路)甲出发半分钟后,乙才从
两地之间为笔直的道路)甲出发半分钟后,乙才从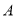 地出发,经过一段时间追上甲,两人继续向
地出发,经过一段时间追上甲,两人继续向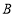 地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向
地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向 地步行,半分钟后与甲相遇,乙又立刻掉头向
地步行,半分钟后与甲相遇,乙又立刻掉头向 地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为
地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为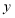 (米)与乙出发的时
(米)与乙出发的时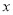 (分钟)之间的关系如图所示,当乙到达
(分钟)之间的关系如图所示,当乙到达 地时,甲与
地时,甲与 地相距的路程是__________米.
地相距的路程是__________米.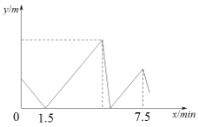
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里,装有四个分别标有数字1、2、3、4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机抽取一个小球,记下数字为y.则小明、小华各取一次小球所确定的数x,y满足y<
 的概率是( )
的概率是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

