【题目】一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.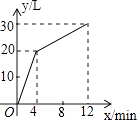
(1)当0≤x≤4时,y关于x的函数解析式为;
(2)当4<x≤12时,求y关于x的函数解析式;
(3)每分钟进水升,每分钟出水升,从某时刻开始的9分钟时容器内的水量是升.
参考答案:
【答案】
(1)y=5x
(2)解:当4<x≤12时,设解析式为y=kx+b(k≠0,k,b为常数),
依题意得 ![]() ,
,
解之得: 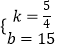 ,
,
∴y= ![]() x+15
x+15
(3)5,![]() ,
,![]()
【解析】解:(1)当0≤x≤4时,y=(20÷4)x=5x,
所以答案是y=5x;
⑶根据图象知道:
每分钟进水20÷4=5升,
每分钟出水[(12﹣4)×5﹣(30﹣20)]÷(12﹣4)= ![]() 升;
升;
∵y= ![]() x+15,
x+15,
当x=9时,y= ![]() ×9+15=
×9+15= ![]() ,
,
∴9分钟时容器内的水量为: ![]() 升.
升.
所以答案是5, ![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1﹣2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.
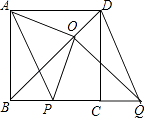
(1)如图,点P在线段BC上,
①求证:四边形APQD是平行四边形;
②判断OA,OP之间的数量关系和位置关系,并加以证明;
(2)若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的中线,
的中线, 是线段
是线段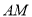 上一点(不与点
上一点(不与点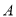 重合).
重合).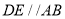 交
交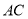 于点
于点 ,
, ,连结
,连结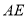 .
.
(1)如图1,当点
 与
与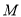 重合时,求证:四边形
重合时,求证:四边形 是平行四边形;
是平行四边形;(2)如图2,当点
 不与
不与 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,延长
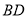 交
交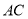 于点
于点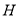 ,若
,若 ,且
,且 .
.①求
 的度数;
的度数;②当
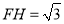 ,
, 时,求
时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】5x3y2﹣xy﹣3x是关于x、y的_____次_____项式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=∠C,点E,F分别在边AB,BC上,AE=DF=DC.
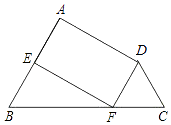
(1)若∠DFC=70°,则∠C的大小=(度),∠B的大小=(度);
(2)求证:四边形AEFD是平行四边形;
(3)若∠FDC=2∠EFB,则四边形AEFD一定是“菱形、矩形、正方形”中的 .
相关试题

