【题目】已知四边形ABCD是正方形,点P,Q在直线BC上,且AP∥DQ,过点Q作QO⊥BD,垂足为点O,连接OA,OP.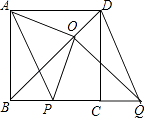
(1)如图,点P在线段BC上,
①求证:四边形APQD是平行四边形;
②判断OA,OP之间的数量关系和位置关系,并加以证明;
(2)若正方形ABCD的边长为2,直接写出BP=1时,△OBP的面积.
参考答案:
【答案】
(1)①证明:∵四边形ABCD是正方形,
∴AD∥BC,
∵AP∥DQ,
∴四边形APQD为平行四边形;
②解:结论:OA=OP,OA⊥OP,理由如下:
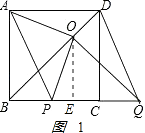
∵四边形ABCD是正方形,
∴AB=BC=PQ,∠ABO=∠OBQ=45°,
∵OQ⊥BD,
∴∠PQO=45°,
∴∠ABO=∠OBQ=∠PQO=45°,
∴OB=OQ,
在△AOB和△OPQ中,
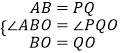 ,
,
∴△AOB≌△POQ(SAS),
∴OA=OP,∠AOB=∠POQ,
∴∠AOP=∠BOQ=90°,
∴OA⊥OP
(2)解:如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,
则BQ=1+2=3,OE= ![]() BQ=
BQ= ![]() ,
,
∴S△OPB= ![]() ×1×
×1× ![]() =
= ![]()
②如图2,当P点在B点左侧时,
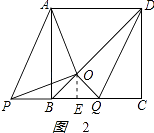
则BQ=2﹣1=1,OE= ![]() BQ=
BQ= ![]() ,
,
∴S△PBO= ![]() ×1×
×1× ![]() =
= ![]() ,
,
综上所述,△POB的面积为 ![]() 或
或 ![]() .
.
【解析】①由四边形ABCD是正方形,得到AD∥BC,已知AP∥DQ,得到四边形APQD为平行四边形;由正方形的性质得AB=BC=PQ,∠ABO=∠OBQ=45°,已知OQ⊥BD,得到∠ABO=∠OBQ=∠PQO=45°,得到OB=OQ,得到△AOB≌△POQ(SAS),得到OA=OP,∠AOB=∠POQ=90°,即OA⊥OP;②当P点在B点右侧时,则BQ=1+2=3,OE= BQ![]() 2= 3
2= 3![]() 2 ,求出△OPB的面积;当P点在B点左侧时,则BQ=2﹣1=1,OE=BQ
2 ,求出△OPB的面积;当P点在B点左侧时,则BQ=2﹣1=1,OE=BQ![]() 2= 1
2= 1![]() 2,求出△OPB的面积.
2,求出△OPB的面积.
【考点精析】本题主要考查了平行四边形的判定与性质和正方形的性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=2x2向左平移1个单位,再向上平移3个单位得到的抛物线,其解析式是( )
A.y=2(x+1)2+3
B.y=2(x﹣1)2﹣3
C.y=2(x+1)2﹣3
D.y=2(x﹣1)2+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
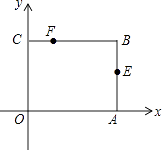
(1)点E的坐标为 , 点F的坐标为;
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为 , 点F′的坐标为;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣1﹣2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的中线,
的中线,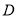 是线段
是线段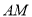 上一点(不与点
上一点(不与点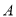 重合).
重合).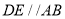 交
交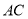 于点
于点 ,
, ,连结
,连结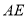 .
.
(1)如图1,当点
 与
与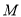 重合时,求证:四边形
重合时,求证:四边形 是平行四边形;
是平行四边形;(2)如图2,当点
 不与
不与 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.(3)如图3,延长
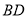 交
交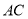 于点
于点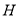 ,若
,若 ,且
,且 .
.①求
 的度数;
的度数;②当
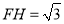 ,
, 时,求
时,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个进水管和与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的函数关系如图所示.
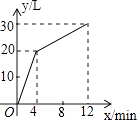
(1)当0≤x≤4时,y关于x的函数解析式为;
(2)当4<x≤12时,求y关于x的函数解析式;
(3)每分钟进水升,每分钟出水升,从某时刻开始的9分钟时容器内的水量是升. -
科目: 来源: 题型:
查看答案和解析>>【题目】5x3y2﹣xy﹣3x是关于x、y的_____次_____项式.
相关试题

