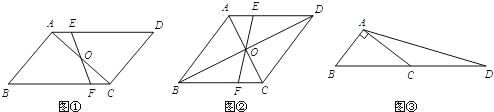
【题目】猜想:如图①,在ABCD中,点O是对角线AC的中点,过点O的直线分别交AD、BC于点E、F.若ABCD的面积是10,则四边形CDEF的面积是 .
探究:如图②,在菱形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F.若AC=4,BD=8,求四边形ABFE的面积.
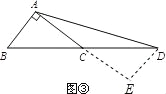
应用:如图③,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD.若AC=4,![]() ,则△ABD的面积是 .
,则△ABD的面积是 .
参考答案:
【答案】5;8;12
【解析】
试题分析:猜想:首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
探究:根据菱形的性质得到AD∥BC,AO=CO,BO=![]() BD=4,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
BD=4,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
应用:延长AC到E使CE=AC=4,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到DE=![]() =3,即可得到结论.
=3,即可得到结论.
试题解析:猜想:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,
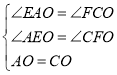 ,
,
∴△AEO≌△CFO,
∴四边形CDEF的面积=S△ACD=![]() ABCD的面积=5;
ABCD的面积=5;
探究:∵四边形ABCD是菱形,
∴AD∥BC,AO=CO,BO=![]() BD=4,
BD=4,
∴∠OAE=∠OCF,∠OEA=∠OFC,
在△AOE于△COF中,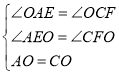 ,
,
∴△AOE≌△COF,
∵AC⊥BD,
∴![]() .
.
应用:延长AC到E使CE=AC=4,
在△ABC与△CDE中,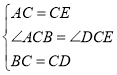 ,
,
∴△ABC≌△CDE,
∴∠E=∠BAC=90°,
∴DE=![]() =3,
=3,
∴S△ABD=S△ADE=![]() AEDE=
AEDE=![]() ×8×3=12.
×8×3=12.
-
科目: 来源: 题型:
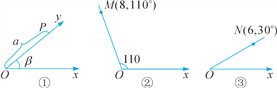
查看答案和解析>>【题目】如图①,将射线Ox按逆时针方向旋转β,得到的射线Oy,如果P为射线Oy上的一点,且OP=a,那么我们规定用(a,β)表示点P在平面内的位置,并记为(a,β).例如,图②中,如果OM=8,∠xOM=110°,那么点M在平面内的位置记为M(8,110°),根据图形,解答下列问题:
(1)如图③,如果点N在平面内的位置记为N(6,30°),那么ON=__ __,∠xON= .
(2)如果点A,B在平面内的位置分别记为A(5,30°),B(12,120°),求A,B两点之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是游乐园的一角.
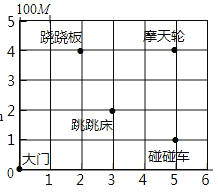
(1)如果用(3,2)表示跳跳床的位置,那么跷跷板用 表示,碰碰车用 表示,摩天轮用 表示.
(2)秋千在大门以东400 m,再往北300 m处,请你在图中标出秋千的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2×(﹣5)+22﹣3+(﹣ )
)
(2)﹣22×(﹣ )+(﹣8)÷(﹣
)+(﹣8)÷(﹣  )3﹣(﹣1)2017
)3﹣(﹣1)2017
(3)先化简,再求值:5a2﹣2b2+2(a2﹣b2)﹣(5a2﹣3b2),其中a= ,b=﹣1.
,b=﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边a、b、c满足(a-5)2+(b-12)2+c2-26c+169=0,则△ABC是___三角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3+(﹣2)﹣(﹣8)﹣(+7)﹣5.
-
科目: 来源: 题型:
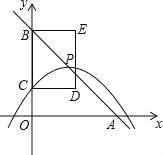
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B.抛物线
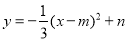 的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.(1)n= (用含m的代数式表示),点C的纵坐标是 (用含m的代数式表示).
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数表达式.
(3)设矩形BCDE的周长为d(d>0),求d与m之间的函数表达式.
(4)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.
相关试题

