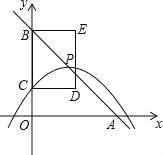
【题目】如图,在平面直角坐标系中,直线y=﹣x+4与x轴、y轴分别交于点A、B.抛物线![]() 的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
的顶点P在直线y=﹣x+4上,与y轴交于点C(点P、C不与点B重合),以BC为边作矩形BCDE,且CD=2,点P、D在y轴的同侧.
(1)n= (用含m的代数式表示),点C的纵坐标是 (用含m的代数式表示).
(2)当点P在矩形BCDE的边DE上,且在第一象限时,求抛物线对应的函数表达式.
(3)设矩形BCDE的周长为d(d>0),求d与m之间的函数表达式.
(4)直接写出矩形BCDE有两个顶点落在抛物线上时m的值.
参考答案:
【答案】(1)﹣m+4,﹣![]() m2﹣m+4;(2)
m2﹣m+4;(2)![]() (3)
(3)![]() ,
,![]() (4)m=1、m=﹣1、
(4)m=1、m=﹣1、![]() 、
、![]()
【解析】
试题分析:(1)根据二次函数的解析式写出顶点P的坐标(m,n),又因为点p在直线y=﹣x+4上,将p点坐标代入可求出n,将二次函数化成一般式后得出点C的纵坐标,并将其化成含m的代数式;
(2)当点P在矩形BCDE的边DE上,且在第一象限时,由CD=2可知,点P的横坐标为2,可求得纵坐标为2,则P(2,2),得出抛物线对应的函数表达式;
(3)根据坐标表示出边BC的长,由矩形周长公式表示出d;
(4)首先点B与C不能重合,因此点B不会在抛物线上,则分两类情况讨论:①点C、D在抛物线上时;②点C、E在抛物线上时;由(1)的结论计算出m的值.
试题解析:(1)y=﹣![]() (x﹣m)2+n=﹣
(x﹣m)2+n=﹣![]() x2+
x2+![]() mx﹣
mx﹣![]() m2+n,
m2+n,
∴P(m,n),
∵点P在直线y=﹣x+4上,
∴n=﹣m+4,
当x=0时,y=﹣![]() m2+n=﹣
m2+n=﹣![]() m2﹣m+4,
m2﹣m+4,
即点C的纵坐标为:﹣![]() m2﹣m+4,
m2﹣m+4,
故答案为:﹣m+4,﹣![]() m2﹣m+4;
m2﹣m+4;
(2)∵四边形BCDE是矩形,
∴DE∥y轴.
∵CD=2,
∴当x=2时,y=2.
∴DE与AB的交点坐标为(2,2).
∴当点P在矩形BCDE的边DE上时,抛物线的顶点P坐标为(2,2).
∴抛物线对应的函数表达式为![]() .
.
(3)∵直线y=﹣x+4与y轴交于点B,
∴点B的坐标是(0,4).
当点B与点C重合时,![]() .
.
解得m1=0,m2=﹣3.
i)当m<﹣3或m>0时,如图①、②,![]()
.![]() .
.

ii)当﹣3<m<0时,如图③,![]() .
.
![]() .
.
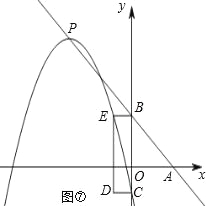
(4)如图④⑤,点C、D在抛物线上时,由CD=2可知对称轴为:x=±1,即m=±1;
如图⑥⑦,点C、E在抛物线上时,由B(0,4)和CD=2得:E(﹣2,4)
则4=﹣![]() (﹣2﹣m)2+(﹣m+4),解得:
(﹣2﹣m)2+(﹣m+4),解得:![]() 、
、![]() .
.



综上所述:m=1、m=﹣1、![]() 、
、![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】猜想:如图①,在ABCD中,点O是对角线AC的中点,过点O的直线分别交AD、BC于点E、F.若ABCD的面积是10,则四边形CDEF的面积是 .
探究:如图②,在菱形ABCD中,对角线AC、BD相交于点O,过点O的直线分别交AD、BC于点E、F.若AC=4,BD=8,求四边形ABFE的面积.
应用:如图③,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD.若AC=4,
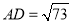 ,则△ABD的面积是 .
,则△ABD的面积是 .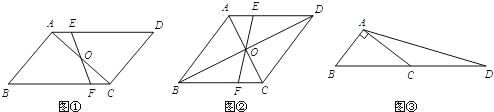
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边a、b、c满足(a-5)2+(b-12)2+c2-26c+169=0,则△ABC是___三角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3+(﹣2)﹣(﹣8)﹣(+7)﹣5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知单项式7amb2与-a4b1-n的和是单项式,那么m-n=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2﹣4x+2=0,下列配方正确的是( )
A.(x+2)2=2B.(x﹣2)2=﹣2C.(x﹣2)2=2D.(x﹣2)2=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某海滩景区门票价格为80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
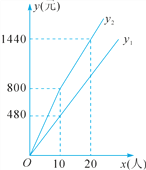
根据图象,回答下列问题:
(1)a= ,b=__ __.
(2)直接写出y1,y2与x之间的函数表达式.
(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到该海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A,B两个旅游团各有多少人.
相关试题

