【题目】解不等式组 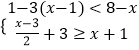 ,并在数轴上表示出其解集.
,并在数轴上表示出其解集.
参考答案:
【答案】解:  ,
,
解不等式①,得x>﹣2,
解不等式②,得x≤1,
把不等式①和②的解集在数轴表示出来如下图所示:
从上图中可看出不等式组的解集为:﹣2<x≤1
【解析】根据一元一次不等式的解法分别解出两个不等式,根据不等式的解集的确定方法得到不等式组的解集.
【考点精析】利用不等式的解集在数轴上的表示和一元一次不等式组的解法对题目进行判断即可得到答案,需要熟知不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
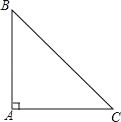
查看答案和解析>>【题目】如图,已知等腰直角△ABC,∠A=90°.
(1)利用尺规作∠ABC的平分线BD,交AC于点D(保留作图痕迹,不写作法);
(2)若将(1)中的△ABD沿BD折叠,则点A正好落在BC边上的A1处,当AB=1时,求△A1DC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
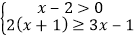 并把解集在数轴上表示出来.
并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个点中在函数y=2x-3的图象上有( )个.
(1,2) , (3,3) , (-1, -1), (1.5,0)
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
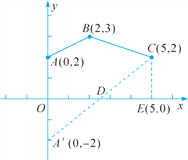
查看答案和解析>>【题目】如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货仓D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D.
(1)试问:在公路边是否存在一点D,使送货路程最短?
(2)求出点D的坐标,并说明理由.
-
科目: 来源: 题型:
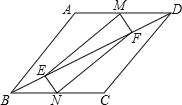
查看答案和解析>>【题目】如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知y1关于x的二次函数y1=ax2+bx+c(a≠0)的图象过点(0,1),且在y轴的左侧,函数值y1随着自变量x的增大而增大.
(1)填空:a 0,b 0,c 0(用不等号连接);
(2)已知一次函数y2=ax+b,当﹣1≤x≤1时,y2的最小值为﹣
 且y1≤1,求y1关于x的函数解析式;
且y1≤1,求y1关于x的函数解析式;(3)设二次函数y1=ax2+bx+c的图象与x轴的一个交点为(﹣1,0),且当a≠﹣1时,一次函数y3=2cx+b﹣a与y4=
 x﹣c(m≠0)的图象在第一象限内没有交点,求m的取值范围.
x﹣c(m≠0)的图象在第一象限内没有交点,求m的取值范围.
相关试题

