【题目】(1)如图![]() 示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.
示,AB∥CD,且点E在射线AB与CD之间,请说明∠AEC=∠A+∠C的理由.

(2)现在如图b示,仍有AB∥CD,但点E在AB与CD的上方,①请尝试探索∠1,∠2,∠E三者的数量关系. ②请说明理由.
参考答案:
【答案】(1)证明见解析(2)∠1+∠2-∠E=180°
【解析】
试题(1)过点E作EF∥AB,由两直线平行,内错角相等,得到∠A=∠1.
由平行的传递性得到EF // CD,再由平行线的性质得到∠2=∠C,由角的和差即可得到结论;
(2)过点E作EF∥AB,类似可得到结论.
试题解析:解:(1)过点E作EF∥AB,∴∠A=∠1(两直线平行,内错角相等).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠2=∠C(两直线平行,内错角相等).
∵∠AEC=∠1+∠2(图上可知),∴∠AEC=∠A+∠C(等量代换) ;
(2)∠1+∠2-∠E=180°.理由如下:
过点E作EF∥AB,∴∠4+∠1=180°(两直线平行,同旁内角互补).
∵AB // CD(已知),∴EF // CD(平行的传递性),∴∠FEC=∠2(两直线平行,内错角相等),即∠3+∠4=∠2,∴∠4=∠2-∠3(等式性质),∴∠2-∠3+∠1=180°(等量代换),
即∠1+∠2-∠AEC=180°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在平面直角坐标系中,点A(3,0),B(0,﹣4),C是x轴上一动点,过C作CD∥AB交y轴于点D.

(1) 的值是 .
的值是 .
(2)若以A,B,C,D为顶点的四边形的面积等于54,求点C的坐标.
(3)将△AOB绕点A按顺时针方向旋转90°得到△AO′B′,设D的坐标为(0,n),当点D落在△AO′B′内部(包括边界)时,求n的取值范围.(直接写出答案即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,∠D=135°,AD=6,CE=
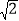 ,点P是线段AC上一点,点F是线段AB上一动点,则PE+PF的最小值是( )
,点P是线段AC上一点,点F是线段AB上一动点,则PE+PF的最小值是( )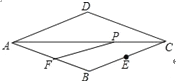
A. 3 B. 6 C. 2
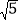 D.
D. 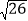
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE、BF、DC是直线,B在直线AC上,E在直线DF上,∠1=∠2,∠A=∠F.
求证:∠C=∠D.

证明:因为∠1=∠2(已知),∠1=∠3( )
得∠2=∠3( )
所以AE//_______( )
得∠4=∠F( )
因为__________(已知)
得∠4=∠A
所以______//_______( )
所以∠C=∠D( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是70cm和48cm,则△ABC的腰和底边长分别为( )
A.24cm和22cm B.26cm和18cm
C.22cm和26cm D.23cm和24cm
-
科目: 来源: 题型:
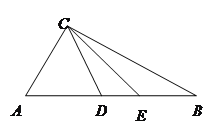
查看答案和解析>>【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点;若△CDE的周长为4,则AB的长为___________;若∠ACB=100°,则∠DCE=_________度;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数
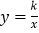 (k>0)的图像上,若OB2-AB2=10,则k的值为 ( )
(k>0)的图像上,若OB2-AB2=10,则k的值为 ( )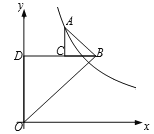
A. 10 B. 5 C. 20 D. 2.5
相关试题

