【题目】已知函数![]() 的图象与
的图象与![]() 轴有两个公共点.
轴有两个公共点.
(1)求![]() 的取值范围,写出当
的取值范围,写出当![]() 取范围内最大整数时函数的解析式;
取范围内最大整数时函数的解析式;
(2)题(1)中求得的函数记为C1
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的值;
的值;
②函数C2:![]() 的图象由函数C1的图象平移得到,其顶点P落在以原
的图象由函数C1的图象平移得到,其顶点P落在以原
点为圆心,半径为![]() 的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
离最大时函数C2的解析式.
参考答案:
【答案】(1)![]() 且
且![]() 当
当![]() 时,函数解析式为:
时,函数解析式为:![]() ;(2)①
;(2)①![]() ;②PM最大时的函数解析式为
;②PM最大时的函数解析式为![]() .
.
【解析】
试题分析: (1)函数![]() 的图象与
的图象与![]() 轴有两个公共点.可知,根的判别式△>0,且m≠0,求得m的范围
轴有两个公共点.可知,根的判别式△>0,且m≠0,求得m的范围![]() 且
且![]() 在此范围内m取得最大整数2,解析式可写出;(2)①根据函数增减性可以发现当x=n时,y=-3n,代入解析式求出
在此范围内m取得最大整数2,解析式可写出;(2)①根据函数增减性可以发现当x=n时,y=-3n,代入解析式求出![]() ;②求出C1的顶点M坐标为
;②求出C1的顶点M坐标为![]()
由图像可知当PM经过圆心O时距离最大,求出直线PM的解析式为![]() 设出P点坐标,根据勾股定理就能求得P点坐标(2,1),C2解析式为
设出P点坐标,根据勾股定理就能求得P点坐标(2,1),C2解析式为![]() .
.
试题解析:(1)由题意可得: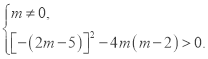 解得:
解得:![]() 且
且![]()
当![]() 时,函数解析式为:
时,函数解析式为:![]() .
.
(2)①函数![]() 图象开口向上,对称轴为
图象开口向上,对称轴为![]()
∴当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
∵当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ,
,
∴ ![]() .
.
∴ ![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
②∵![]()
∴图象顶点![]() 的坐标为
的坐标为![]() ,
,
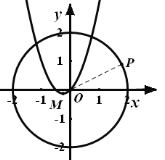
由图形可知当![]() 为射线
为射线![]() 与圆的交点时,距离最大.
与圆的交点时,距离最大.
∵点P在直线OM上,由![]() 可求得直线解析式为:
可求得直线解析式为:![]() ,
,
设P(a,b),则有a=2b,
根据勾股定理可得![]()
求得![]() .
.
∴PM最大时的函数解析式为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:
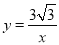
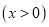 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是
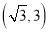 ,点N的坐标是
,点N的坐标是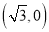 时,求点P 的坐标;
时,求点P 的坐标; (2) 如图3,当点M的坐标是
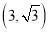 ,点N的坐标是
,点N的坐标是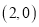 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.



-
科目: 来源: 题型:
查看答案和解析>>【题目】连续四次抛掷一枚硬币都是正面朝上,则“第五次抛掷正面朝上”是( )
A.必然事件B.不可能事件C.随机事件D.小概率事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b<0,b>0,则下列结论:①a>b>0;②|a|<|b|;③ab<0;④b﹣a>b+a,正确的是( )
A. ①②B. ②③C. ③④D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式﹣3amb2与abn+1和的结果仍然是单项式,则m﹣n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
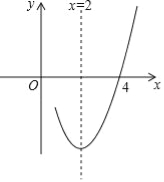
A.①②③ B.③④⑤ C.①②④ D.①④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】4 的平方根是 ( )
A. 2 B. -2 C. 16 D. ±2
相关试题

