【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:![]()
![]() 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.
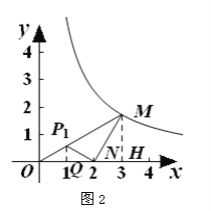
(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求点P 的坐标;
时,求点P 的坐标;
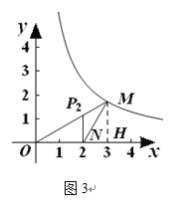
(2) 如图3,当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;
(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.



参考答案:
【答案】(1)![]() ;(2)
;(2)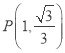 或
或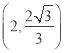 ;(3)存在,
;(3)存在,![]()
【解析】
试题分析:(1)易证点P是三角形MON的自相似点,过点P作PD⊥x轴于D点根据M、N坐标易知∠MNO=90°,再利用三角函数可求出P点坐标![]() ;(2)根据坐标发现ON=MN=2,要找自相似点只能在∠ONM中做∠ONP=∠OMN或∠MNP=∠MON,分别画出图形,根据图形性质,结合相似可求出自相似点的坐标;(3)根据前两问可发现,要想有自相似点,其实质就是在大角里面做小角,当三个角都相等时,即△OMN为等边三角形时,不存在自相似点,因此可得到直线OM的解析式y=
;(2)根据坐标发现ON=MN=2,要找自相似点只能在∠ONM中做∠ONP=∠OMN或∠MNP=∠MON,分别画出图形,根据图形性质,结合相似可求出自相似点的坐标;(3)根据前两问可发现,要想有自相似点,其实质就是在大角里面做小角,当三个角都相等时,即△OMN为等边三角形时,不存在自相似点,因此可得到直线OM的解析式y=![]() x,与
x,与![]() 的交点就是M,从而可以求得N的坐标.
的交点就是M,从而可以求得N的坐标.
试题解析:(1)在△ONP和△OMN中,
∵∠ONP=∠OMN,∠NOP=∠MON
∴△ONP∽△OMN
∴点P是△M0N的自相似点.
过点P作PD⊥x轴于D点.
![]()
∴![]() .
.
∵![]() ,
,
∴![]() , ∴
, ∴![]() .
.
在Rt△OPN中,![]() .
.
![]() .
.
![]() . ∴
. ∴![]() .
.
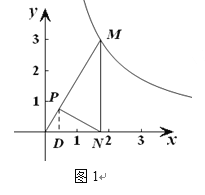
(2)①如图2,过点M作MH⊥x轴于H点,
∵ ![]() ,
,![]()
∴![]() ,直线OM的表达式为
,直线OM的表达式为![]() .
.![]()
∵![]() 是△M0N的自相似点,∴△
是△M0N的自相似点,∴△![]() ∽△NOM
∽△NOM
过点![]() 作
作![]() ⊥x轴于Q点,
⊥x轴于Q点,
∴![]()
∵![]() 的横坐标为1,∴
的横坐标为1,∴![]() ∴
∴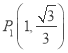 .
.
如图3,△![]() ∽△NOM ,
∽△NOM ,
∴![]() ∴
∴![]() .
.
∵![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ∴
∴![]() ,
,
∴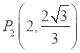 .
.
综上所述,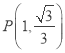 或
或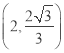 .
.
(3)存在,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形中,属于分解因式的是( )
A.a(x+y)=ax+ay
B.x2﹣4x+4=x(x﹣4)+4
C.10x2﹣5x=5x(2x﹣1)
D.x2﹣16+6x=(x+4)(x﹣4)+6x -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①a一定是一个正数;②圆柱的上下两底面是大小相等的圆,侧面是平面;③棱柱的各条棱都相等;④几个有理数的积等于0,那么其中至少有一个因数为0,其中正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中为必然事件的是( )
A.打开电视机,正在播放茂名新闻
B.早晨的太阳从东方升起
C.随机掷一枚硬币,落地后正面朝上
D.下雨后,天空出现彩虹 -
科目: 来源: 题型:
查看答案和解析>>【题目】连续四次抛掷一枚硬币都是正面朝上,则“第五次抛掷正面朝上”是( )
A.必然事件B.不可能事件C.随机事件D.小概率事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b<0,b>0,则下列结论:①a>b>0;②|a|<|b|;③ab<0;④b﹣a>b+a,正确的是( )
A. ①②B. ②③C. ③④D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象与
的图象与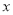 轴有两个公共点.
轴有两个公共点.(1)求
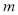 的取值范围,写出当
的取值范围,写出当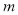 取范围内最大整数时函数的解析式;
取范围内最大整数时函数的解析式;(2)题(1)中求得的函数记为C1
①当
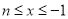 时,
时,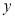 的取值范围是
的取值范围是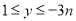 ,求
,求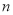 的值;
的值;②函数C2:
 的图象由函数C1的图象平移得到,其顶点P落在以原
的图象由函数C1的图象平移得到,其顶点P落在以原 点为圆心,半径为
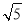 的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距
的圆内或圆上.设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
相关试题

