【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,P是△ABC内一点,PA=1,PB=3,PC=![]() .求∠CPA的度数.
.求∠CPA的度数.

参考答案:
【答案】135°
【解析】由于△ABC为等腰直角三角形,AB=AC,则把△APB绕A点逆时针旋转90°可得到△AP′C,连PP′,根据旋转的性质得到∠P′AP=90°,P′A=PA=1,P′C=PB=3,得到△PAP′为等腰直角三角形,根据等腰直角三角形的性质得P′P=![]() PA=
PA=![]() ,∠APP′=45°,在△P′PC中,可得到PC2+P′P2=P′C2,根据勾股定理的逆定理得到△P′PC为直角三角形,∠CPP′=90°,利用∠CPA=∠CPP′+∠APP′进行计算即可.
,∠APP′=45°,在△P′PC中,可得到PC2+P′P2=P′C2,根据勾股定理的逆定理得到△P′PC为直角三角形,∠CPP′=90°,利用∠CPA=∠CPP′+∠APP′进行计算即可.
∵△ABC为等腰直角三角形,AB=AC,
∴把△APB绕A点逆时针旋转90°可得到△AP′C,连PP′,如图,
∴∠P′AP=90°,P′A=PA=1,P′C=PB=3,
∴△PAP′为等腰直角三角形,
∴P′P=![]() PA=
PA=![]() ,∠APP′=45°,
,∠APP′=45°,
在△P′PC中,P′C=3,P′P=![]() ,PC=
,PC=![]() ,
,
∵(![]() )2+(
)2+(![]() )2=32,
)2=32,
∴PC2+P′P2=P′C2,
∴△P′PC为直角三角形,∠CPP′=90°,
∴∠CPA=∠CPP′+∠APP′=90°+45°=135°.
“点睛”本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理的逆定理以及等腰直角三角形的判定与性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形腰上的高与底边夹角为15°,则顶角的度数为 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=(2﹣m)x+2的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.

(1)用含a、b、r的式子表示阴影部分面积(结果保留π);
(2)当a=10,b=6,r=2时,计算阴影部分的面积.(π取3.14,结果精确到0.1) -
科目: 来源: 题型:
查看答案和解析>>【题目】能说明命题“关于x的一元二次方程x2+mx+4=0,当m<﹣2时必有实数解”是假命题的一个反例为( )
A.m=﹣4
B.m=﹣3
C.m=﹣2
D.m=4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.
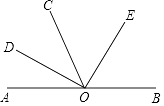
(1)求∠BOD的度数.
(2)试判断OE是否平分∠BOC,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=3时,代数式ax2-3x-4的值为5,则字母a的值为________.
相关试题

