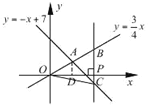
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

参考答案:
【答案】(1)A(4,3);(2)28.
【解析】试题分析:(1)点A是正比例函数![]() 与一次函数
与一次函数![]() 图像的交点坐标,把
图像的交点坐标,把![]() 与
与![]() 联立组成方程组,方程组的解就是点A的横纵坐标;(2)过点A作x轴的垂线,在Rt△OAD中,由勾股定理求得OA的长,再由BC=
联立组成方程组,方程组的解就是点A的横纵坐标;(2)过点A作x轴的垂线,在Rt△OAD中,由勾股定理求得OA的长,再由BC=![]() OA求得OB的长,用点P的横坐标a表示出点B、C的坐标,利用BC的长求得a值,根据
OA求得OB的长,用点P的横坐标a表示出点B、C的坐标,利用BC的长求得a值,根据![]() 即可求得△OBC的面积.
即可求得△OBC的面积.
试题解析:解:(1)由题意得,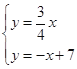 ,解得
,解得![]() ,
,
∴点A的坐标为(4,3).
过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理得,
![]() ,
,
∴![]() .
.
∵P(a,0),∴B(a,![]() ),C(a,-a+7),∴BC=
),C(a,-a+7),∴BC=![]() ,
,
∴![]() ,解得a=8.
,解得a=8.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】无论a取何值,关于x的函数y=﹣x+a2+1的图象都不经过( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】苹果进价是每千克x元,要得到10%的利润,则该苹果售价应是每千克_____元(用含x的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
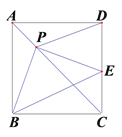
(1)求证:BP=EP;
(2)若CE=3,BE=6,求∠CPE的度数;
(3)探究AP、PC、BE之间的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某图书馆2015年年底有图书10万册,预计2017年年底有图书14.4万册.求这两年图书册数的年平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在1.17-32-23中把省略的“+”号填上应得到( )
A. 1.17+32+23
B. -1.17+(-32)+(-23)
C. 1.17+(-32)+(-23)
D. 1.17-(+32)-(+23)
-
科目: 来源: 题型:
查看答案和解析>>【题目】地图上某地的面积为100cm2,比例尺是l:500,则某地的实际面积是_______m2.
相关试题

