【题目】在平面直角坐标系中,如果直线 y=kx 与函数 y= 的图象恰有 3 个不同的交点,则 k的取值范围是_________.
的图象恰有 3 个不同的交点,则 k的取值范围是_________.
参考答案:
【答案】![]() <k<2
<k<2
【解析】
根据题意把y=kx分别代入各个分段函数解析式,用k表示出x的值,再根据x的取值范围确定k的范围.
解:①∵直线y=kx与函数y=2x+4有交点,
∴kx=2x+4,
∴x=![]() ,
,
又∵x<﹣3,
即![]() ,
,
当k﹣2>0,即k>2时,解得k![]() ,
,
此时无解.
当k﹣2<0,即k<2时,解得k![]() ,
,
∴![]() ,
,
②∵直线y=kx与函数y=﹣2有交点,
∴kx=﹣2,
∴x=![]() ,
,
又∵﹣3≤x≤3,
即﹣3≤![]() ≤3,
≤3,
解得:k![]() ,
,
③∵直线y=kx与函数y=2x﹣8有交点,
∴kx=2x﹣8,
∴x=![]() ,
,
又∵x>3,
即![]() ,
,
解得:k![]() ,
,
综上所述:![]() .
.
故答案为:![]() <k<2.
<k<2.
-
科目: 来源: 题型:
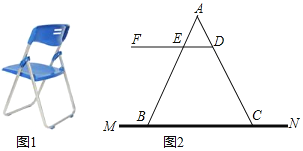
查看答案和解析>>【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图
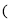 图
图 ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得 厘米,
厘米,  厘米,
厘米,  .
. 求椅子的高度
求椅子的高度 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离 精确到1厘米
精确到1厘米
 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离 精确到1厘米
精确到1厘米 参考数据:
参考数据: 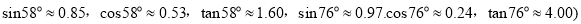
-
科目: 来源: 题型:
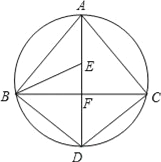
查看答案和解析>>【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(+17)+(-12);
(2)10+(―
 )―6―(―0.25);
)―6―(―0.25);(3)(
 )×48 ;
)×48 ;(4)|-5-4|-5×(-2)2-1÷(-
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 13×7 的网格中,每个小正方形边长都是 1,其顶点叫做格点,如图 A、B、D、E 均为格点,
 ABD 为格点三角形.
ABD 为格点三角形.
(1)请在给定的网格中画 ABCD,要求 C 点在格点上;
(2)在(1)中 ABCD 右侧,以格点 E 为其中的一个顶点,画格点
 EFG,并使 EF=5,FG=3,EG=
EFG,并使 EF=5,FG=3,EG=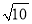
(3)先将(2)中的线段 EF 向右平移 6 个单位、再向下平移 l 个单位到 MP 的位置,再以 MP 为对角线画矩形 MNPQ(M、N、P、Q 按逆时针方向排列),直接写出矩形 MNPQ 的面积为 ______
-
科目: 来源: 题型:
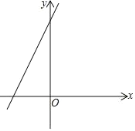
查看答案和解析>>【题目】如图,直线l:y=2x+4
(1)①直接写出直线l关于y轴对称的直线l1的解析式_______.
②直接写出直线l向右平移2个单位得到的直线l2的解析式________.
(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l1于点Q、交直线l2于点P.若PM=2PQ,求M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果
 ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )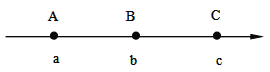
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
相关试题

