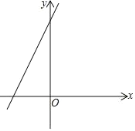
【题目】如图,直线l:y=2x+4
(1)①直接写出直线l关于y轴对称的直线l1的解析式_______.
②直接写出直线l向右平移2个单位得到的直线l2的解析式________.
(2)在(1)的基础上,点M是x轴上一点,过点M作x轴的垂线交直线l1于点Q、交直线l2于点P.若PM=2PQ,求M点的坐标.
参考答案:
【答案】(1)①y=﹣2x+4;②y=2x;(2)M(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)①先求出点A,B坐标,再利用对称性求出点C坐标,最后利用待定系数法即可得出结论;
②利用平移的性质即可得出结论;
(2)设出点M坐标,进而表示出点P,Q坐标,即可表示出PM,PQ,最后建立方程求解即可得出结论.
解:①如图,记直线y=2x+4与y轴的交点为A,与x轴的交点为B,
∴A(﹣2,0),B(0,4),
∴点A关于y轴的对称点C的坐标为(2,0),
设直线l1的解析式的解析式为y=kx+4,
∴2k+4=0,
∴k=﹣2,
∴直线l1的解析式y=﹣2x+4;
②直线l:y=2x+4向右平移2个单位得到的直线l2的解析式y=2(x﹣2)+4=2x,
故答案为:y=﹣2x+4,y=2x;
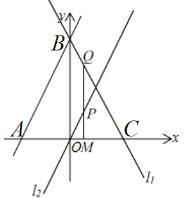
(2)如图,
设点M(m,0),
∵点P在直线l2:y=2x上,
∴P(m,2m),
∵点Q在直线l1:y=﹣2x+4上,
∴Q(m,﹣2m+4),
∴PM=|2m|,PQ=|2m﹣(﹣2m+4)|=4|m﹣1|,
∵PM=2PQ,
∴|2m|=2×4|m﹣1|,
∴m=![]() 或m=
或m=![]() ,
,
∴M(![]() ,0)或(
,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(+17)+(-12);
(2)10+(―
 )―6―(―0.25);
)―6―(―0.25);(3)(
 )×48 ;
)×48 ;(4)|-5-4|-5×(-2)2-1÷(-
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,如果直线 y=kx 与函数 y=
 的图象恰有 3 个不同的交点,则 k的取值范围是_________.
的图象恰有 3 个不同的交点,则 k的取值范围是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 13×7 的网格中,每个小正方形边长都是 1,其顶点叫做格点,如图 A、B、D、E 均为格点,
 ABD 为格点三角形.
ABD 为格点三角形.
(1)请在给定的网格中画 ABCD,要求 C 点在格点上;
(2)在(1)中 ABCD 右侧,以格点 E 为其中的一个顶点,画格点
 EFG,并使 EF=5,FG=3,EG=
EFG,并使 EF=5,FG=3,EG=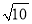
(3)先将(2)中的线段 EF 向右平移 6 个单位、再向下平移 l 个单位到 MP 的位置,再以 MP 为对角线画矩形 MNPQ(M、N、P、Q 按逆时针方向排列),直接写出矩形 MNPQ 的面积为 ______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果
 ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )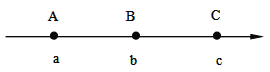
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,AE⊥AB交BC于点D,交⊙O于点E,F在DA的延长线上,且AF=AD.若AF=3,tan∠ABD=
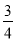 ,求⊙O的直径.
,求⊙O的直径.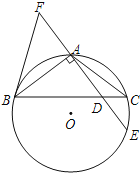
-
科目: 来源: 题型:
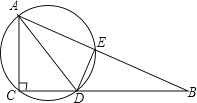
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD外接圆的直径.
相关试题

