【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).

(1)求抛物线的解析式;
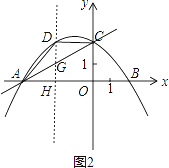
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.
参考答案:
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2;(2)2,D的坐标为(﹣2,2);(3)y=
x+2;(2)2,D的坐标为(﹣2,2);(3)y=![]() x﹣
x﹣![]() 或y=﹣
或y=﹣![]() x﹣
x﹣![]() .
.
【解析】试题分析:
(1)由已知条件可设抛物线解析式为: ![]() ,再代入点C的坐标(0,2)解得
,再代入点C的坐标(0,2)解得![]() 的值即可得到抛物线的解析式;
的值即可得到抛物线的解析式;
(2)如图2,过点D作DH⊥AB于H,交直线AC于点G,由A、C的坐标求出直线AC的解析式,设点D的横坐标为“m”,则可用含“m”的代数式表达出DG的长,结合S△ADC=![]() DG×OA即可用“m”的式子表达出其面积,配方即可得到当“m”为何值时,面积最大,并得到面积的最大值;
DG×OA即可用“m”的式子表达出其面积,配方即可得到当“m”为何值时,面积最大,并得到面积的最大值;
(3)如图3,设过点E的直线与⊙M相切于点F,与x轴交于点N,连接MF,则有MF⊥EN,由已知条件易得:⊙M的半径为3,点M的坐标为:(﹣1,0),ME=5,在Rt△MFE中可求得EF=4;再证△MEF∽△NEM,由两三角形对应边成比例可求得MN=![]() ,从而可求得点N的坐标为(
,从而可求得点N的坐标为( ![]() ,0)或(
,0)或(![]() ,0),结合点E的坐标即可求得直线NE的解析式.
,0),结合点E的坐标即可求得直线NE的解析式.
试题解析:
(1)抛物线![]() 与
与![]() 轴交于A(﹣4,0),B(2,0),
轴交于A(﹣4,0),B(2,0),
∴可设![]() ,
,
又∵抛物线过点C(0,2),
∴![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为: ![]() ;
;
(2)过点D作DH⊥AB于H,交直线AC于点G,如图2.
设直线AC的解析式为![]() ,由已知可得:
,由已知可得: ![]() ,
,
解得: 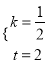 ,
,
∴直线AC的解析式为![]() .
.
设点D的横坐标为m,则点G的横坐标也为m,
∴DH=![]() ,GH=
,GH=![]() ,
,
∴DG=DH-GH= ![]() ,
,
∴S△ADC=![]() DG·OA
DG·OA
=![]()
=![]()
=![]() ,
,
∵点D在直线AC上方的抛物线上,
∴![]() ,
,
∴当m=﹣2时,S△ADC取到最大值2.
此时yD=![]() ,
,
∴点D的坐标为(﹣2,2);
(3)设过点E的直线与⊙M相切于点F,与x轴交于点N,连接MF,如图3,
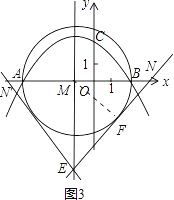
则有MF⊥EN.
∵A(﹣4,0),B(2,0),
∴AB=6,MF=MB=MA=3,
∴点M的坐标为:(﹣1,0).
∵E(﹣1,﹣5),
∴ME=5,∠EMN=90°.
∴在Rt△MFE中,EF=![]() .
.
∵∠MEF=∠NEM,∠MFE=∠EMN=90°,
∴△MEF∽△NEM,
∴![]() ,即:
,即: ![]() ,
,
解得:NM=![]() ,
,
∴点N的坐标为(![]() ,0)即(
,0)即( ![]() ,0)或(
,0)或(![]() ,0)即(
,0)即(![]() ,0).
,0).
设直线EN的解析式为y=px+q.
①当点N的坐标为( ![]() ,0)时,由题意可得:
,0)时,由题意可得: 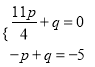 ,
,
解得: 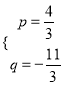 ,
,
∴直线EN的解析式为![]() .
.
②当点N的坐标为(![]() ,0)时,
,0)时,
同理可得:直线EN的解析式为: ![]() .
.
综上所述:所求直线的解析式为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车同时从A地出发,匀速开往B地.甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动;当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h.设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.
(1)A、B两地的距离是______km,乙车的速度是______km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距150km时,直接写出x的值.

-
科目: 来源: 题型:
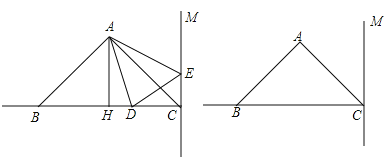
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 上部分点的横坐标
上部分点的横坐标 , 纵坐标
, 纵坐标 的对应值如下表:
的对应值如下表:
…


0
1
2
…

…
0
4
6
6
4
…
从上表可知,下列说法正确的是 .
①抛物线与
 轴的一个交点为
轴的一个交点为 ; ②抛物线与
; ②抛物线与 轴的交点为
轴的交点为 ;
;③抛物线的对称轴是:直线
 ; ④在对称轴左侧
; ④在对称轴左侧 随
随 增大而增大.
增大而增大. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.

(1)求证:DE是⊙O的切线;
(2)如图AD=5,AE=4,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
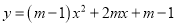
(1)m= 时,函数图像与x轴只有一个交点;
(2)m为何值时,函数图像与x轴没有交点;
(3)若函数图像与x轴交于A、B两点,与y轴交于点C,且△ABC的面积为4,求m的值.
相关试题

