【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.
参考答案:
【答案】①②④正确
【解析】试题分析:根据表中的数据可知x=-2时,y=0,据此即可判断①,由表中数据可知x=0时,y=6,据此即可判断②,根据x=-1和x=2时,y=4,可知抛物线上点(-1,4)和点(2,4)关于抛物线的对称轴对称,根据对称性即可得出抛物线的对称轴,据此即可判断③,结合对称轴和二次函数的性质即可判断④.
试题解析:
解:从表中知道:当x=-2时,y=0,当x=0时,y=6,
∴抛物线与x轴的一个交点为(-2,0),抛物线与y轴的交点为(0,6),
所以①②正确;
从表中还知道:当x=-1和x=2时,y=4,
∴抛物线的对称轴方程为x=![]() =
=![]() ,
,
所以③错误;
∵a=-1<0,抛物线开口向下,在对称轴x=![]() 的左侧y随x的增大而增大,
的左侧y随x的增大而增大,
∴在对称轴左侧y随x增大而增大,
故④正确.
所以①②④正确.
-
科目: 来源: 题型:
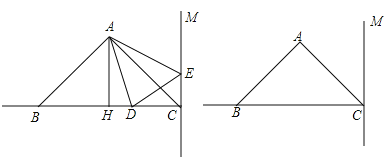
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).

(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.

(1)求证:DE是⊙O的切线;
(2)如图AD=5,AE=4,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
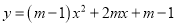
(1)m= 时,函数图像与x轴只有一个交点;
(2)m为何值时,函数图像与x轴没有交点;
(3)若函数图像与x轴交于A、B两点,与y轴交于点C,且△ABC的面积为4,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,DC⊥BC,AE 平分∠BAD,DE 平分∠ADC,以下结论:①∠AED=90°;②点 E 是 BC 的中点;③DE=BE;④AD=AB+CD;其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
相关试题

