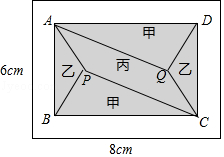
【题目】小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.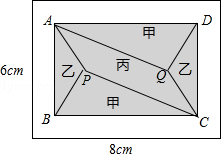
(1)若区域Ⅰ的三种瓷砖均价为300元/m2 , 面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2 , 且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足AB:BC=2:3,区域Ⅱ四周宽度相等
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2 , 乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
参考答案:
【答案】
(1)
解:由题意300S+(48﹣S)200≤12000,
解得S≤24.
∴S的最大值为24.
(2)
解:①设区域Ⅱ四周宽度为a,则由题意(6﹣2a):(8﹣2a)=2:3,解得a=1,
∴AB=6﹣2a=4,CB=8﹣2a=6.
②设乙、丙瓷砖单价分别为5x元/m2和3x元/m2,则甲的单价为(300﹣3x)元/m2,
∵PQ∥AD,
∴甲的面积=矩形ABCD的面积的一半=12,设乙的面积为s,则丙的面积为(12﹣s),
由题意12(300﹣3x)+5xs+3x(12﹣s)=4800,
解得s= ![]() ,
,
∵0<s<12,
∴0< ![]() <12,
<12,
∴0<x<50,
∴丙瓷砖单价3x的范围为0<3x<150元/m2.
【解析】(1)根据题意可得300S+(48﹣S)200≤12000,解不等式即可;(2)①设区域Ⅱ四周宽度为a,则由题意(6﹣2a):(8﹣2a)=2:3,解得a=1,由此即可解决问题;②设乙、丙瓷砖单价分别为5x元/m2和3x元/m2 , 则甲的单价为(300﹣3x)元/m2 , 由PQ∥AD,可得甲的面积=矩形ABCD的面积的一半=12,设乙的面积为s,则丙的面积为(12﹣s),由题意12(300﹣3x)+5xs+3x(12﹣s)=4800,解得s= ![]() ,由0<s<12,可得0<
,由0<s<12,可得0< ![]() <12,解不等式即可;
<12,解不等式即可;
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过抛物线y=
 x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长
 (单位长度)。慢车长
(单位长度)。慢车长 (单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点
(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点 为原点,取向右方向为正方向画数轴,此时快车
为原点,取向右方向为正方向画数轴,此时快车 在数轴上表示的数是
在数轴上表示的数是 ,慢车头
,慢车头 在数轴上表示的数是
在数轴上表示的数是 ,若快车
,若快车 以
以 个单位长度/秒的速度向右匀速继续行驶,同时慢车
个单位长度/秒的速度向右匀速继续行驶,同时慢车 以
以 个单位长度/秒的速度向左匀速继续行驶,且
个单位长度/秒的速度向左匀速继续行驶,且 与
与 互为相反数.
互为相反数.(1)求此时刻快车头
 与慢车头
与慢车头 之间相距多少单位长度?
之间相距多少单位长度?(2)从此时刻开始算起,问再行驶多少秒两列火车行驶到车头
 、
、 相距
相距 个单位长度?
个单位长度?(3)此时在快车
 上有一位爱到脑筋的七年级学生乘客
上有一位爱到脑筋的七年级学生乘客 ,他发现行驶中有一段时间,他的位置
,他发现行驶中有一段时间,他的位置 到两列火车头
到两列火车头 、
、 的距离和加上到两列火车尾
的距离和加上到两列火车尾 、
、 的距离和是一个不变的值(即
的距离和是一个不变的值(即 为定值),你认为学生
为定值),你认为学生 发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.
发现的这一结论是否正确?若正确,求出增定值及所持续的时间;若不正确,请说明理由.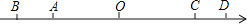
附加题:
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数
60≤x<90
90≤x<120
120≤x<150
150≤x<180
180≤x<210
频数
16
25
9
7
3
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几(精确到0.1%)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:
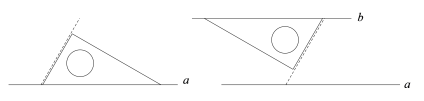
①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
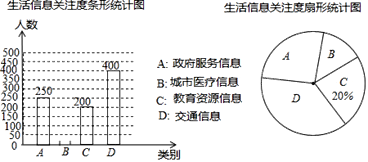
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:
种类
频数
频率
卡通画
a
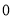 .45
.45时文杂志
b
0.16
武侠小说
50
c
文学名著
d
e
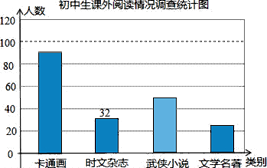
(1)这次随机调查了______名学生,统计表中a=______,d=______;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是______;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
相关试题

