【题目】抛物线![]() 与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
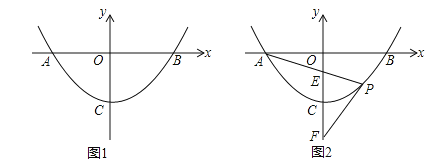
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
参考答案:
【答案】(1)①![]() ;②D(﹣1,﹣3)或(
;②D(﹣1,﹣3)或(![]() ,
,![]() );(2)定值为2.
);(2)定值为2.
【解析】
试题分析:(1)①根据待定系数法求函数解析式,可得答案;②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;
(2)根据待定系数法,可得E、F点的坐标,根据分式的性质,可得答案.
试题解析:(1)①将P(1,﹣3),B(4,0)代入![]() ,得:
,得:![]() ,解得:
,解得: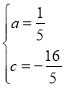 ,抛物线的解析式为
,抛物线的解析式为![]() ;
;
②如图1,由∠DPO=∠POB,得:DP∥OB,D与P关于y轴对称,P(1,﹣3),得D(﹣1,﹣3);
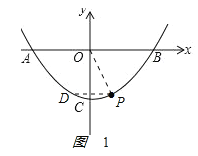
如图,D在P右侧,即图中D2,则∠D2PO=∠POB,延长PD2交x轴于Q,则QO=QP,设Q(q,0),则![]() ,解得:q=5,∴Q(5,0),则直线PD2为
,解得:q=5,∴Q(5,0),则直线PD2为![]() ,再联立
,再联立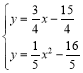 ,解得:x=1或
,解得:x=1或![]() ,∴ D2(
,∴ D2(![]() ,
,![]() ).
).
综上所述,点D的坐标为(-1,-3)或(![]() ,
,![]() ).
).

(2)点P运动时,![]() 是定值,设P点坐标为(m,
是定值,设P点坐标为(m,![]() ),A(﹣4,0),B(4,0),设AP的解析式为y=kx+b,将A、P点坐标代入,得:
),A(﹣4,0),B(4,0),设AP的解析式为y=kx+b,将A、P点坐标代入,得: ,解得b=
,解得b=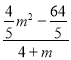 =
=![]() ,即E(0,
,即E(0,![]() ),设BP的解析式为y=k1x+b1,将B、P点坐标代入,得:
),设BP的解析式为y=k1x+b1,将B、P点坐标代入,得:
,解得b2= =
=![]() ,即F(0,
,即F(0,![]() ),OF+OE=
),OF+OE=![]() =
=![]() ,
,![]() =
=![]() =2.
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:

(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了还是减少了?增多或减少了多少元?请说明理由.
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )

A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,种植草莓不超过20亩时,所得利润y(元)与种植面积m(亩)满足关系式y=1500m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数、反比例函数或二次函数中的一种).

(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量的取值范围;
(2)如果小王家计划承包40亩荒山种植草莓和樱桃,当种植樱桃面积x(亩)满足0<x<20时,求小王家总共获得的利润w(元)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=∠COD=90°,OE平分∠AOC,∠AOD=120°.

(1)求∠BOC的度数;
(2)求∠BOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知xm=5,xn=7,求x2m+n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .
相关试题

