搜索
【题目】已知xm=5，xn=7，求x2m+n的值．
参考答案：
【答案】解：∵xm=5，xn=7，
∴x2m+n=xmxmxn=5×5×7=175
【解析】根据同底数幂的乘法，即可解答．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为支持国家南水北调工程建设，小王家由原来养殖户变为种植户，经市场调查得知，种植草莓不超过20亩时，所得利润y（元）与种植面积m（亩）满足关系式y=1500m；超过20亩时，y=1380m+2400．而当种植樱桃的面积不超过15亩时，每亩可获得利润1800元；超过15亩时，每亩获得利润z（元）与种植面积x（亩）之间的函数关系如下表（为所学过的一次函数、反比例函数或二次函数中的一种）．
（1）设小王家种植x亩樱桃所获得的利润为P元，直接写出P关于x的函数关系式，并写出自变量的取值范围；
（2）如果小王家计划承包40亩荒山种植草莓和樱桃，当种植樱桃面积x（亩）满足0＜x＜20时，求小王家总共获得的利润w（元）的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线
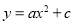与x轴交于A，B两点，顶点为C，点P为抛物线上，且位于x轴下方．（1）如图1，若P（1，﹣3），B（4，0）．
①求该抛物线的解析式；
②若D是抛物线上一点，满足∠DPO=∠POB，求点D的坐标；
（2）如图2，已知直线PA，PB与y轴分别交于E、F两点．当点P运动时，
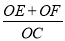是否为定值？若是，试求出该定值；若不是，请说明理由．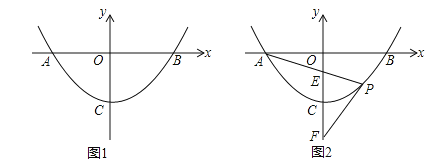
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠AOB=∠COD=90°，OE平分∠AOC，∠AOD=120°．
（1）求∠BOC的度数；
（2）求∠BOE的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=（a﹣1）x2﹣x+a2﹣1 的图象经过原点，则a的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解刚生产的10 000台电视机的寿命情况，从中抽取100台电视机进行实验，这个问题中的样本容量是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
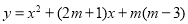（m为常数，﹣1≤m≤4）．A（﹣m﹣1，
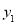），B（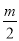
，
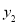），C（﹣m，
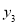）是该抛物线上不同的三点，现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a，过抛物线顶点P作PH⊥a于H．（1）用含m的代数式表示抛物线的顶点坐标；
（2）若无论m取何值，抛物线与直线y=x﹣km（k为常数）有且仅有一个公共点，求k的值；
（3）当1＜PH≤6时，试比较
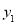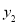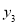，，之间的大小．
相关试题
