【题目】如图,在平面直角坐标系内,已知点A(0,6),点B(8,0).动点P从A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P,Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似,并求出此时点P的坐标.

参考答案:
【答案】(1)y=﹣![]() x+6;(2)当t为
x+6;(2)当t为![]() 秒或
秒或![]() 秒时,△APQ与△AOB相似
秒时,△APQ与△AOB相似
【解析】试题分析:(1)设直线AB的解析式为y=kx+b,解得k,b即可;
(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t;②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.
试题解析:解:(1)设直线AB的解析式为y=kx+b,由题意得:
![]() ,解得:
,解得: 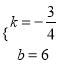 .
.
∴直线AB的解析式为y=﹣![]() x+6;
x+6;
(2)在Rt△AOB中,AO=6,BO=8,根据勾股定理得:AB=10.
由题意知:AP=t,AQ=10﹣2t.分两种情况讨论:
①当∠APQ=∠AOB时.∵∠A=∠A,∴△APQ∽△AOB,∴ ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
②当∠AQP=∠AOB时.∵∠A=∠A,∴△AQP∽△AOB,∴ ![]() ,∴t=
,∴t=![]() (秒).
(秒).
综上所述:当t为![]() 秒或
秒或![]() 秒时,△APQ与△AOB相似.
秒时,△APQ与△AOB相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,∠A=45,BD⊥AD,BD=2
(1)求平行四边形ABCD的周长和面积
(2)求A、C两点间的距离

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(-
 )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|- |÷(
|÷( -
- )×(-4)2.
)×(-4)2.(3)(
 -
- +
+ )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1- )÷3×[2-(-3)2].
)÷3×[2-(-3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的初中数学应用能力竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将八年级的一班和二班的成绩整理并绘制成如下的统计图,二班D级共有4人.

请你根据以上提供的信息解答下列问题:
(1)求此竞赛中一班共有多少人参加比赛,并补全条形统计图.
(2)扇形统计图中A级对应的圆心角度数是 .
(3)此次竞赛中二班在C级以上(包括C级)的人数为 .
(4)请你将表格补充完成:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O为坐标原点,已知直线
 经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB(1)求直线
 的函数解析式
的函数解析式(2)若直线
 也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两城间的铁路路程为1600千米,经过技术改造,列车实施了提速,提速后比提速前速度增加了20千米/小时,列车从甲城到乙城行驶时间减少4小时,这条铁路在现有条件下安全行驶速度不得超过140千米/小时,请你用学过的知识说明在这条铁路的现有条件下列车是否还可以再提速。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律.例如:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为
 .请利用以上结论解决下列问题.
.请利用以上结论解决下列问题.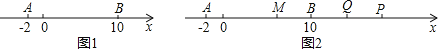
(1)如图1,数轴上点A表示的数为﹣2,点B表示的数为10,则A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
(2)数轴上另有一动点P从点A出发,以每秒4个单位长度的速度沿数轴向右匀速运动,点Q是线段BP的中点.设运动时间为t秒:
①当t=2时,求此时点Q表示的数;
②如图2,点P运动至B点右侧,M是线段AQ的中点,若B恰好是QM的中点,求t的值.
相关试题

